LE NOTE SU QUESTA PARTE SONO STATE AGGIORNATE- SI VEDA SEZIONE INIZIALE SU MOODLE

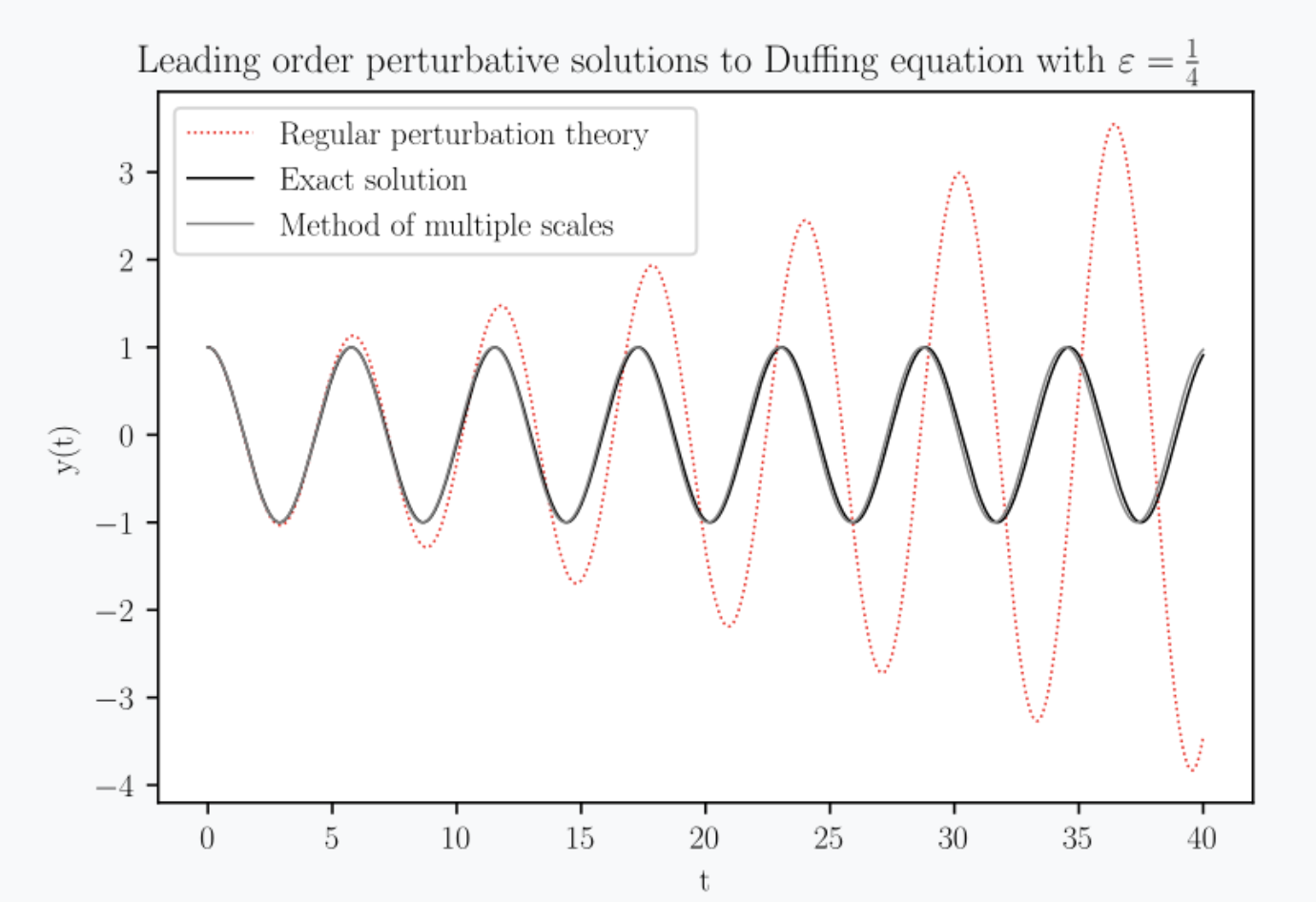
Nella figura: confronto tra teoria perturbativa standard, che da un risultato completamente errato, e approssimazione del prim'ordine ottenuta con il metodo delle scale multiple, per l'equazione di Duffing. 

in questa lezione abbiamo finito di descrivere il metodo dei boundary layers, sullo stesso esempio della scorsa lezione e anche considerando un'equazione leggermente piu` complessa , epsilon y''(x) + (1+x ) y'(x) + y(x) = 0, con y(0) = y(1) = 1, per la quale abbiamo calcolato l'approsimazione del prim'ordine con il metodo delle due espansioni asintotiche (interna e esterna al boundary layer) incollate.

In seguito, abbiamo descritto il metodo delle scale multiple, sull'esempio dell'equazione di Duffing y''(t) + y(t) + epsilon y^3(t) = 0, con condizioni iniziali y(0) = 1, y'(0) = 0. Abbiamo mostrato come il metodo delle scale multiple possa essere usato per rimuovere i termini "secolari", e portare all'approssimazione del prim'ordine y(t) = cos(t + 3/8 epsilon t ).