Abbiamo studiato il metodo delle curve caratteristiche per equazioni quasi -lineari con alcuni esempi, in particolare considerando problemi con condizioni iniziali date su una curva (problema di Cauchy).

Abbiamo visto come, anche se la soluzione e` solo data in forma implicita (non sempre e` possibile invertire la parametrizzazione data dalle curve caratteristiche), si puo` sempre usarla per generare un grafico delle soluzioni. Per alcuni esempi di grafici generati in questo modo in Mathematica si veda il file pdf allegato. 

Abbiamo discusso le condizioni che garantiscono l'esistenza e unicita` locale delle soluzioni del problema di Cauchy (problema delle condizioni iniziali su una curva). Abbiamo visto un esempio in cui le condizioni del teorema sono violate e infatti la soluzione diventa a due valori in un intorno della curva di Cauchy.

Abbiamo poi discusso l'equazione di Burgers inviscida (o equazione del trasporto nonlineare), che e` un prototipo dell'importante fenomeno di formazione degli shock dovuto alla nonlinearita`.

Abbiamo brevemente discusso il ruolo di questa equazione come analogo delle equazioni di Eulero nel caso di una dimensione spaziale (e una temporale). 

Abbiamo poi discusso la soluzione dell'equazione di Burgers con profilo iniziale arbitrario, mostrando come in molti casi l'evoluzione temporale porta alla formazione di una singolarita` in cui il gradiente della soluzione u_x diverge. Abbiamo discusso come calcolare il tempo in cui avviene questa singolarita`, e come dopo questo istante la soluzione diventi a piu` valori.

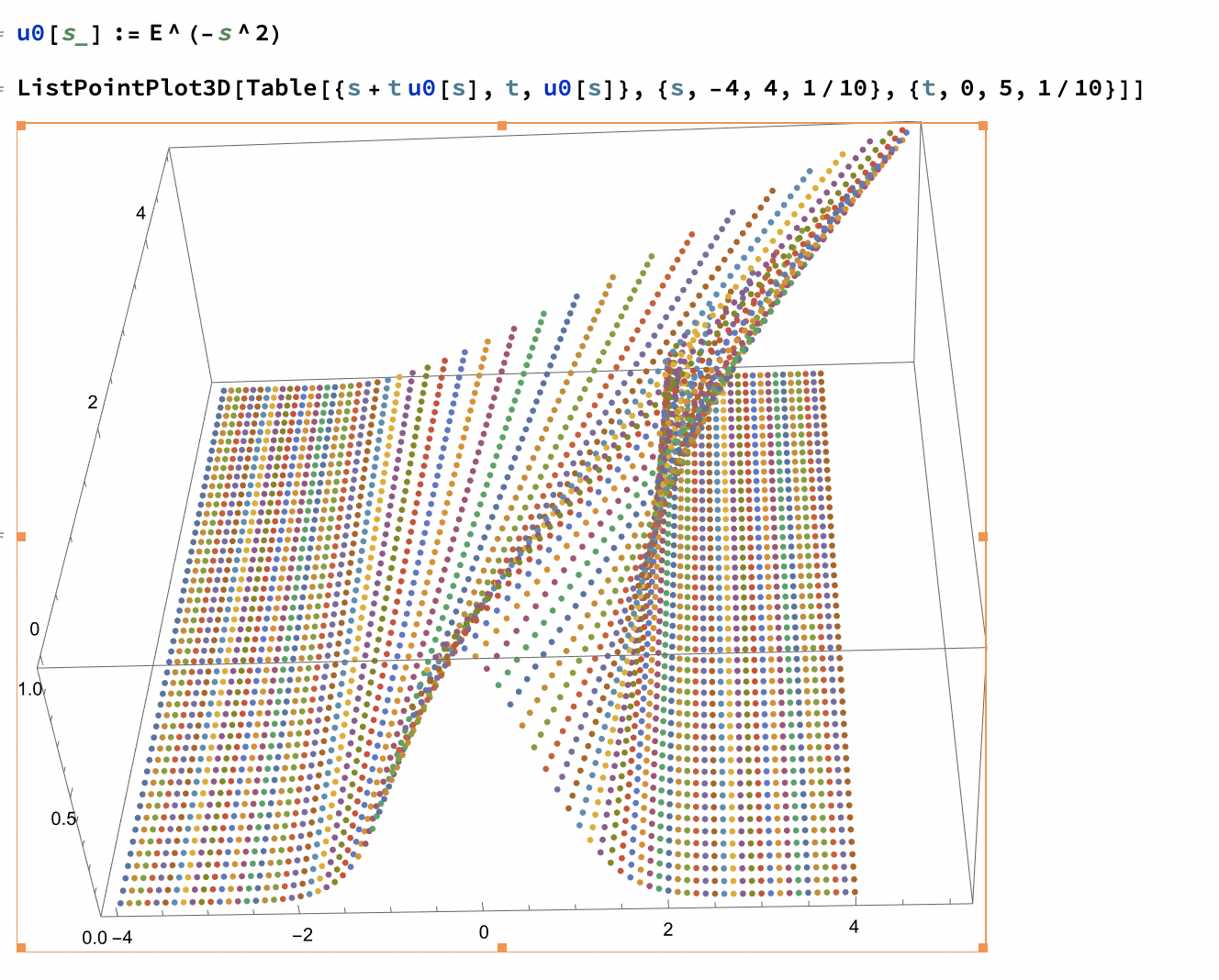Fenomeno di formazione di una singolarita` per una soluzione dell'equazione di Burgers inviscida, con profilo iniziale gaussiano, risolta con il metodo delle caratteristiche. I semplici comandi in Mathematica illustrano come realizzare il grafico della soluzione a tempi generici. Sopo la formazione della singolarita` la soluzione diventa a piu` valori.