Section outline
-
-
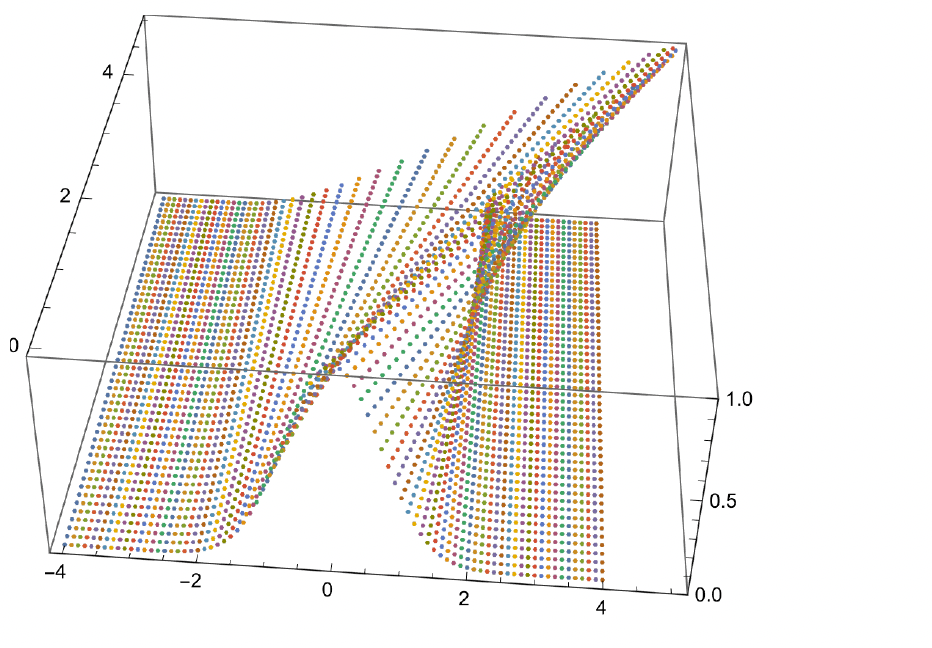
Il codice permette di produrre il grafico della soluzione, dato un certo profilo iniziale, usando il metodo delle caratteristiche, in particolare usa la soluzione per le curve caratteristiche vista a lezione. (Il programma e` scitto in Mathematica, ma si puo` facilmente adattare a altri programmi di calcolo simbolico, ad esempio Python che e` open access).