章节大纲

    • registrazione lezione 网页地址

    • Abbiamo finito di discutere il problema della soluzione dell'equazione di Laplace in un semipiano e discusso la soluzione dell'equazione di Laplace (problema di Dirichlet( in vari domini con simmetrie particolari che permettano di usare il metodo di decomposizione in autofunzioni. Abbiamo brevemente illustrato l'uso delle mappe tra funzioni olomorfe per risolvere l'equazione di Laplace in un dominio generico nel piano. Senza discutere i dettagli formali, questo e` stato illustrato con un esempio della mappa tra il problema di Neumann all'esterno di un cerchio e all'esterno di un dominio ellittico. 






    • file usato per generare i grafici delle linee di flusso intorno a ostacolo circolare e ellittico 文件

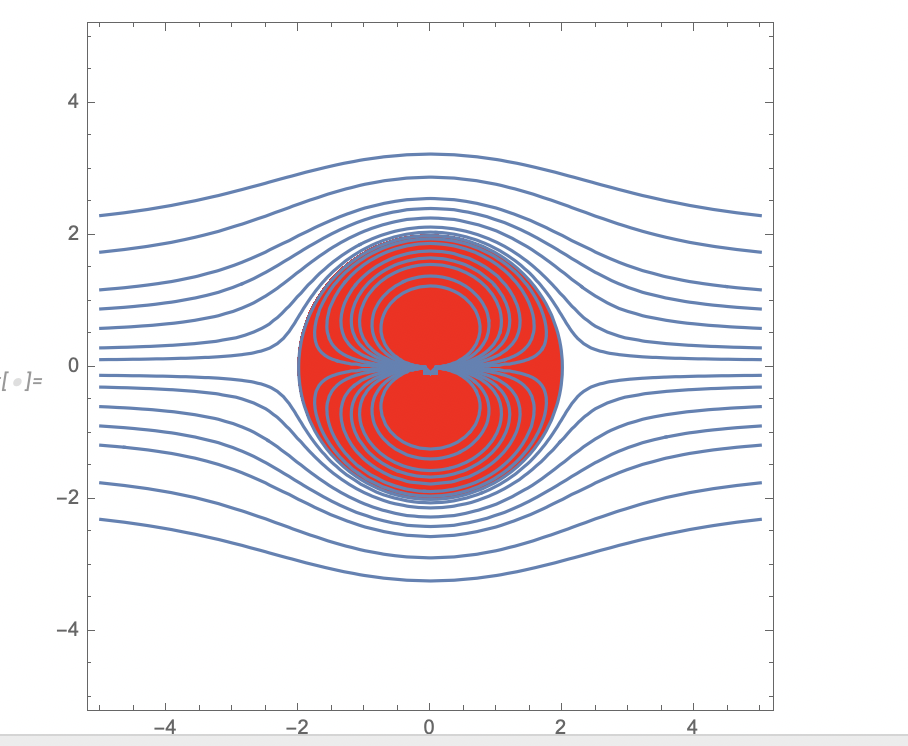
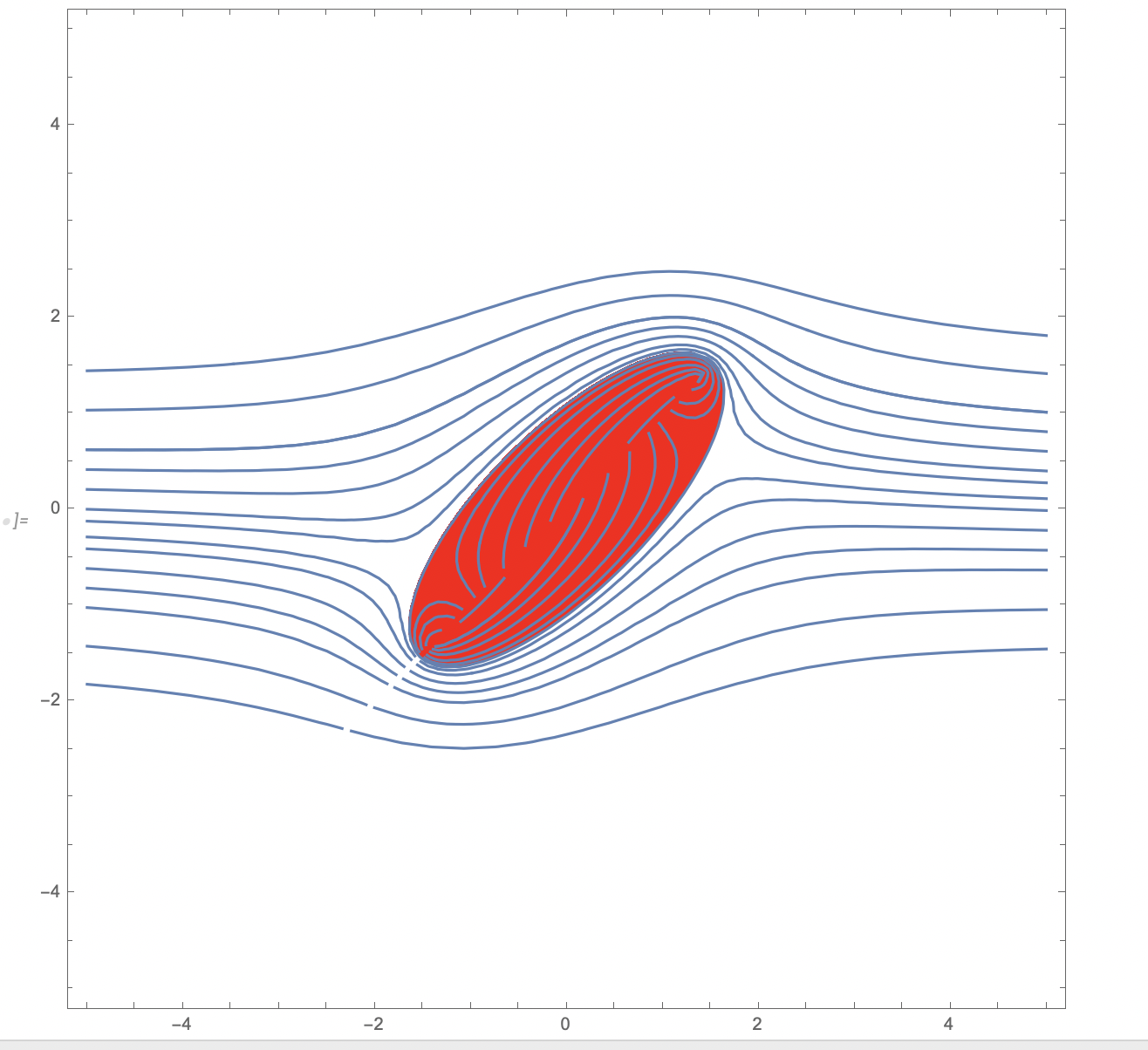
      I dettagli matematici della mappa conforme usata non sono importanti per l'esame. Le osservazioni importanti sono che le linee di flusso (parallele al gradiente del potenziale del flusso) sono ottenute come curve di livello della parte immaginaria della funzione complessa associata, dove la parte reale rappresenta il potenziale del flusso. Inoltre e` importante la comprensione del principio generale per cui facendo una composizione di mappa olomorfe si possono costruire soluzioni dell'equazione di Laplace in dominii diversi.