章节大纲
-
-
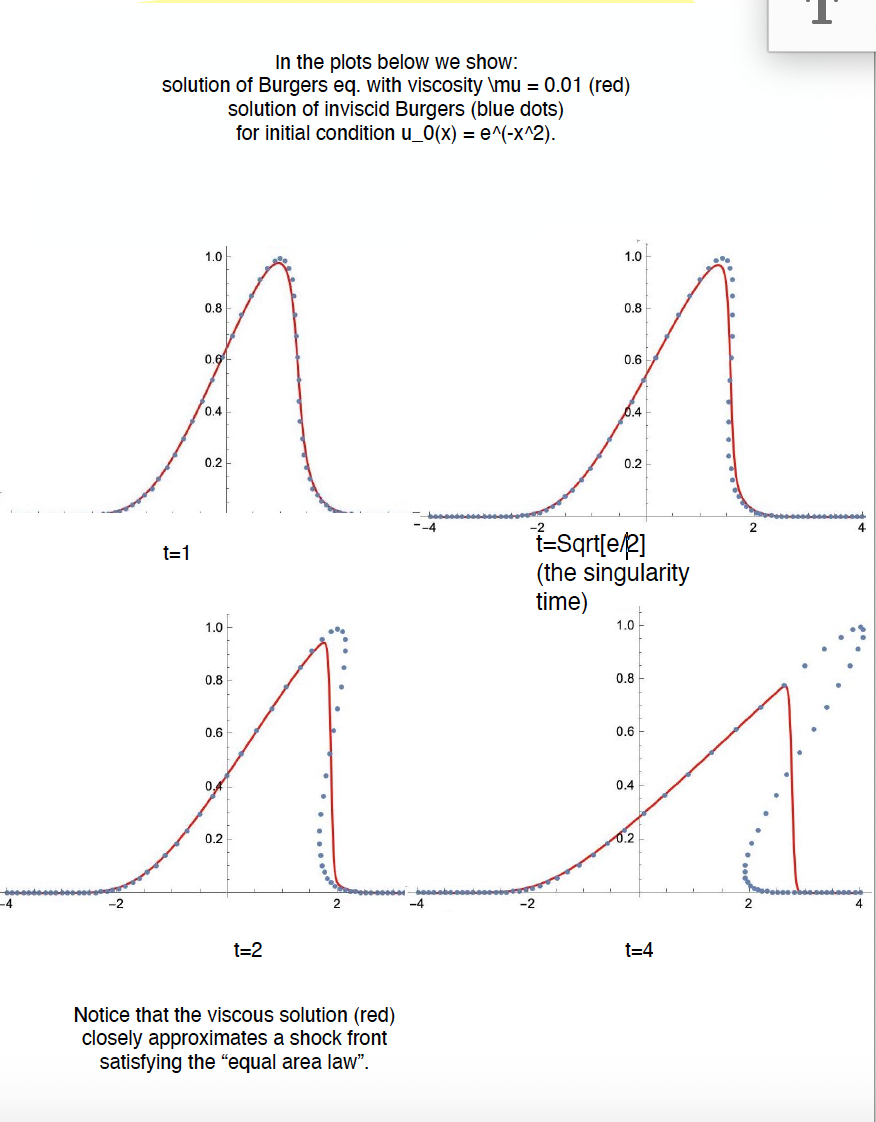
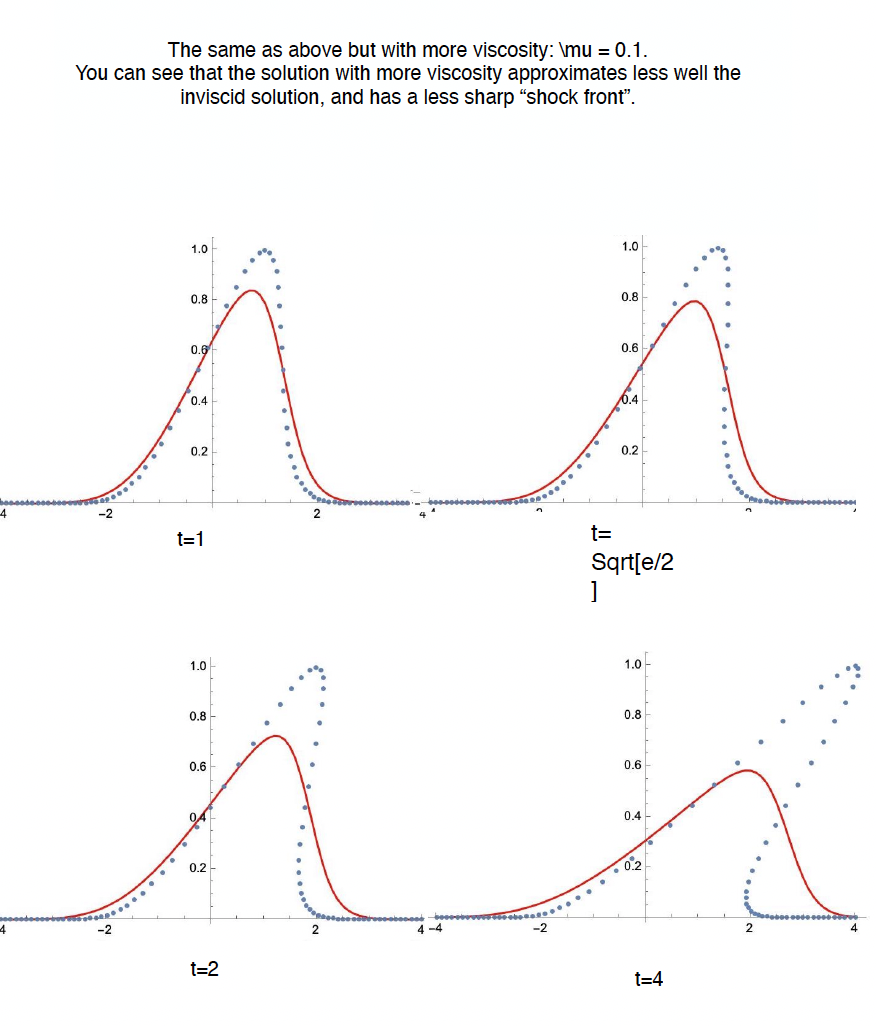
Purtroppo ci sono stati dei problemi tecnici nella registrazione di alcune parti della prima parte della lezione. Gli appunti corrispondenti si trovano nella parte delle note sull'equazione di Burgers con viscosita` (verso la fine delle note dello scorso anno).
Le altre parti registrate si trovano ai link:
- https://unito.webex.com/recordingservice/sites/unito/recording/f8385b0a7677103caffbbe32b373da81/playback
- Seconda parte della lezione: https://unito.webex.com/recordingservice/sites/unito/recording/f8385b0a7677103caffbbe32b373da81/playback
-