Section outline
-
-
Sono state aggiornate le note del corso.
-
-
-
Elenco dei cambiamenti rispetto alle note del 2023-2024. Si veda anche la pagina campusnet per un riassunto dettagliato degli argomenti che abbiamo trattato.
-
Questa parte delle note e` quasi identica a quelle del 2022-2023. E` stato aggiunto il calcolo di un integrale calcolato sul cammino "Pac-Man", discusso a lezione.
-
Rispetto alle note del 2023-2024, e` stata aggiunta una parte piu` dettagliata sul metodo di Laplace (o metodo del punto a sella). Sono state trattate solo le funzioni Gamma, Zeta e Ipergeometriche generalizzate, mentre non sono state trattate le funzioni Poligamma e i Polilogaritmi.
-
E` stata aggiunta alle note una parte sui problemi di bordo per equazioni lineari, ed espansa la parte sulle funzioni di Green (il contenuto della lezione 8).
-
NOTA: Rispetto alle note dello scorso anno, non e` piu` presente la parte sul metodo di Papperitz-Riemann.
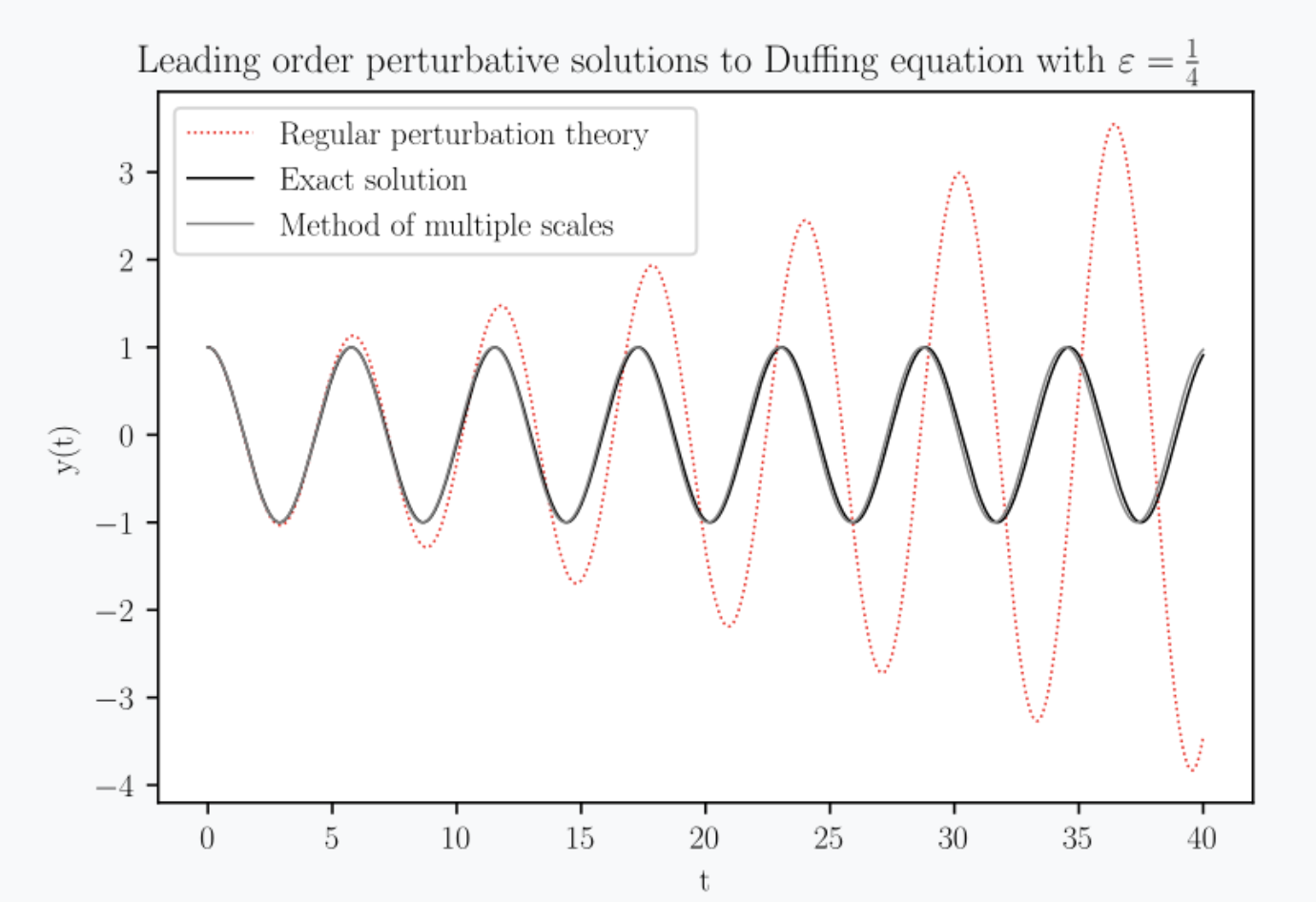
NEW: Sono presenti due parti nuove (lezioni 10-11) su metodi perturbativi in casi singolari: il metodo dei boundary layers e il metodo delle scale multiple. Questi metodi non saranno oggetto di esercizi ma faranno parte degli argomenti possibili di discussione all'orale. Si noti anche il metodo di espansione intorno a punti irregolari singolari, che puo` essere argomento di esercizi per l'esame scritto.
-
Questa parte delle note e` la stessa rispetto a quelle del 2023-2024. Nota: l'argomento principale della lezione 15, cioe` la trattazione degli shock e delle soluzioni deboli dell'equazione di Burgers e` contenuta in una parte successiva delle note.
-
NEW: E` stata aggiunta la discussione delle funzioni di Green, trattata nella lezione 17.
-
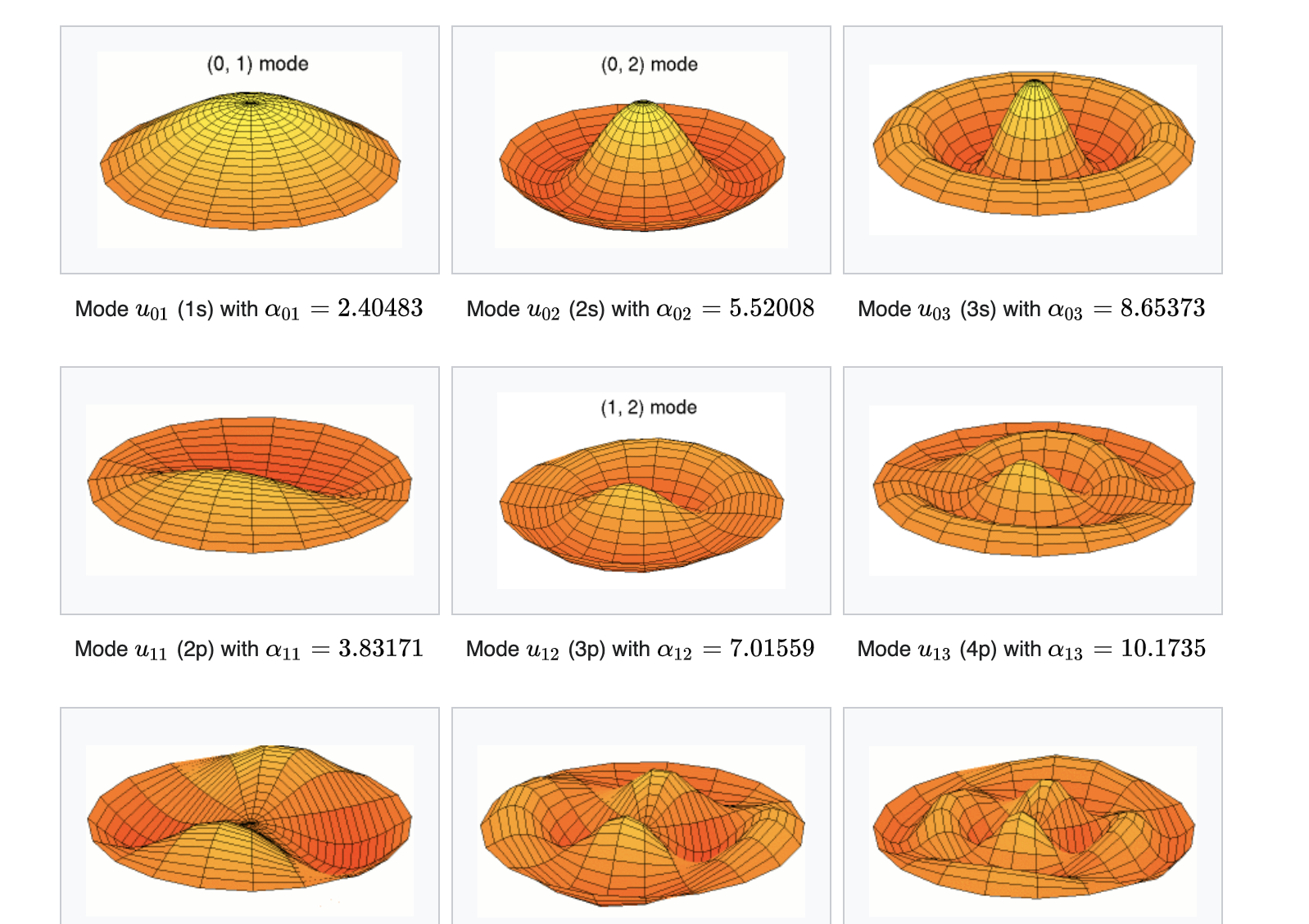
Questa parte delle note e` identica a quella del 2023-2024. Le note includono anche la trattazione delle soluzioni dell'equazione di Helmholtz in dominio sferico, che NON sono state trattate quest' anno. Abbiamo trattato solo il caso del dominio cilindrico, con l'esempio dello studio delle oscillazioni di una membrana circolare.
-
Rispetto alle note dello scorso anno, ci sono piccoli cambiamenti: e` stata aggiornata la parte delle note sulla relazione tra soluzione fondamentale (heat kernel) e funzione di Green, e sono state fatte piccole correzioni di sviste in alcune formule nella parte sulla separazione delle variabili.
Si noti che l'ultima parte del documento sui problemi matematicamente ben posti o mal posti NON e` stata discussa a lezione e non e` parte del programma.
-
Questa parte delle note e` identica a quelle del 2023-2024.
-
Questa parte delle note e` identica al 2023-2024. NOTA: il metodo delle immagini e` stato trattato solo nel caso del semi-piano, non nel caso del disco. Nel caso del disco e` importante pero` saper risolvere il problema con il metodo delle autofunzioni.
-
-
-
Si vedano in particolare le note dell'ultimo capitolo su funzioni di Green nelle PDE.
-
-
-
link a cartella con il video.
-
-
-
-
Articolo del famoso fisico matematico Michael Berry
-
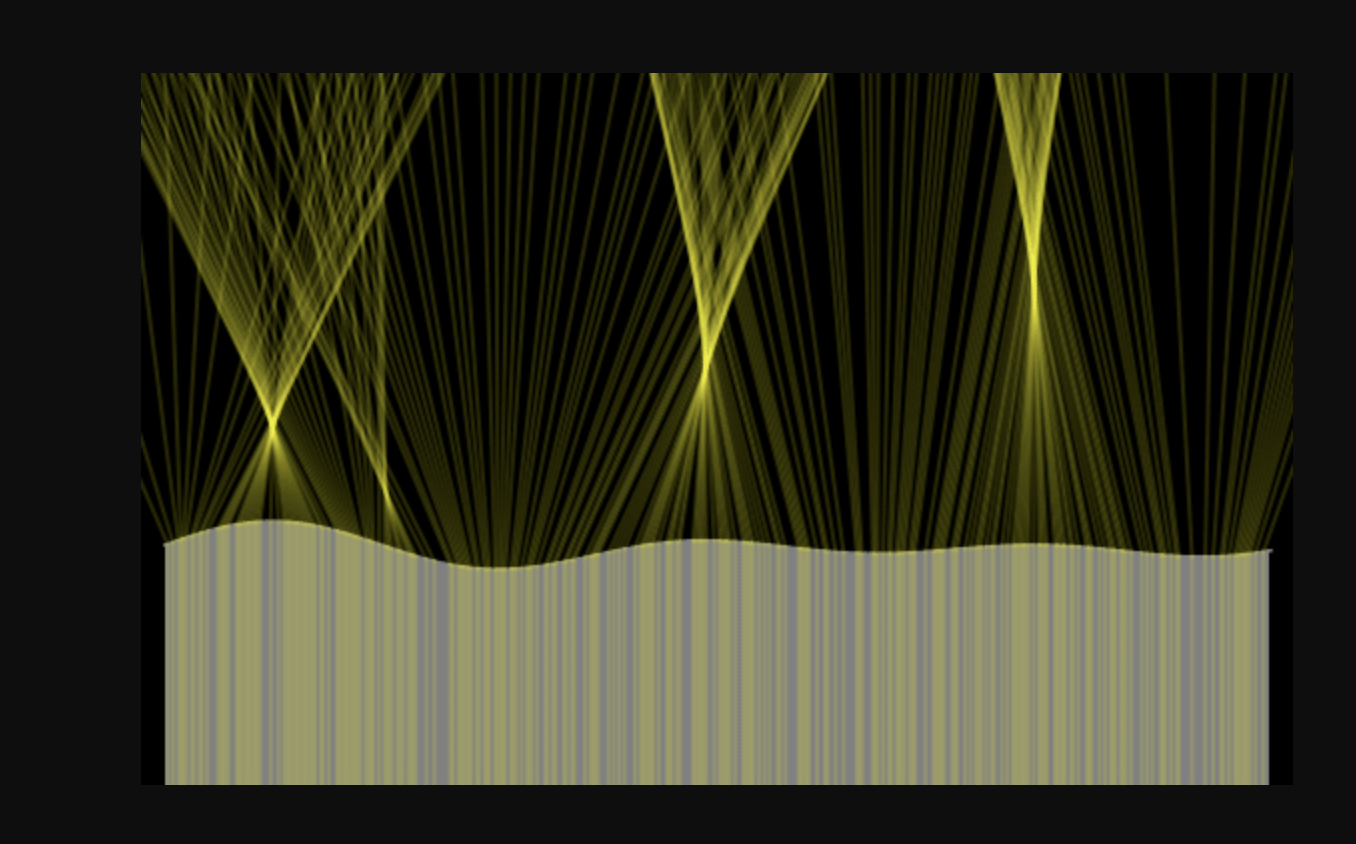
Spiegazione della derivazione della funzione oscillante di Airy per il profilo intensita` della luce dell'arcobaleno in funzione dell'angolo rispetto all'orizzonte. Spiega la comparsa delle frange sovranumerarie sotto l'arcobaleno principale.
-
Con un qualsiasi programma di calcolo simbolico (Maple, Mathematica, Python (open access), o molti altri), si puo` facilmente adattare il programma per generare una soluzione dell'equazione di Burgers con profilo iniziale a piacere. Il metodo si puo` generalizzare per risolvere nello stesso modo, con il metodo delle curve caratteristiche, qualsiasi PDE con derivate del prim'ordine.
-
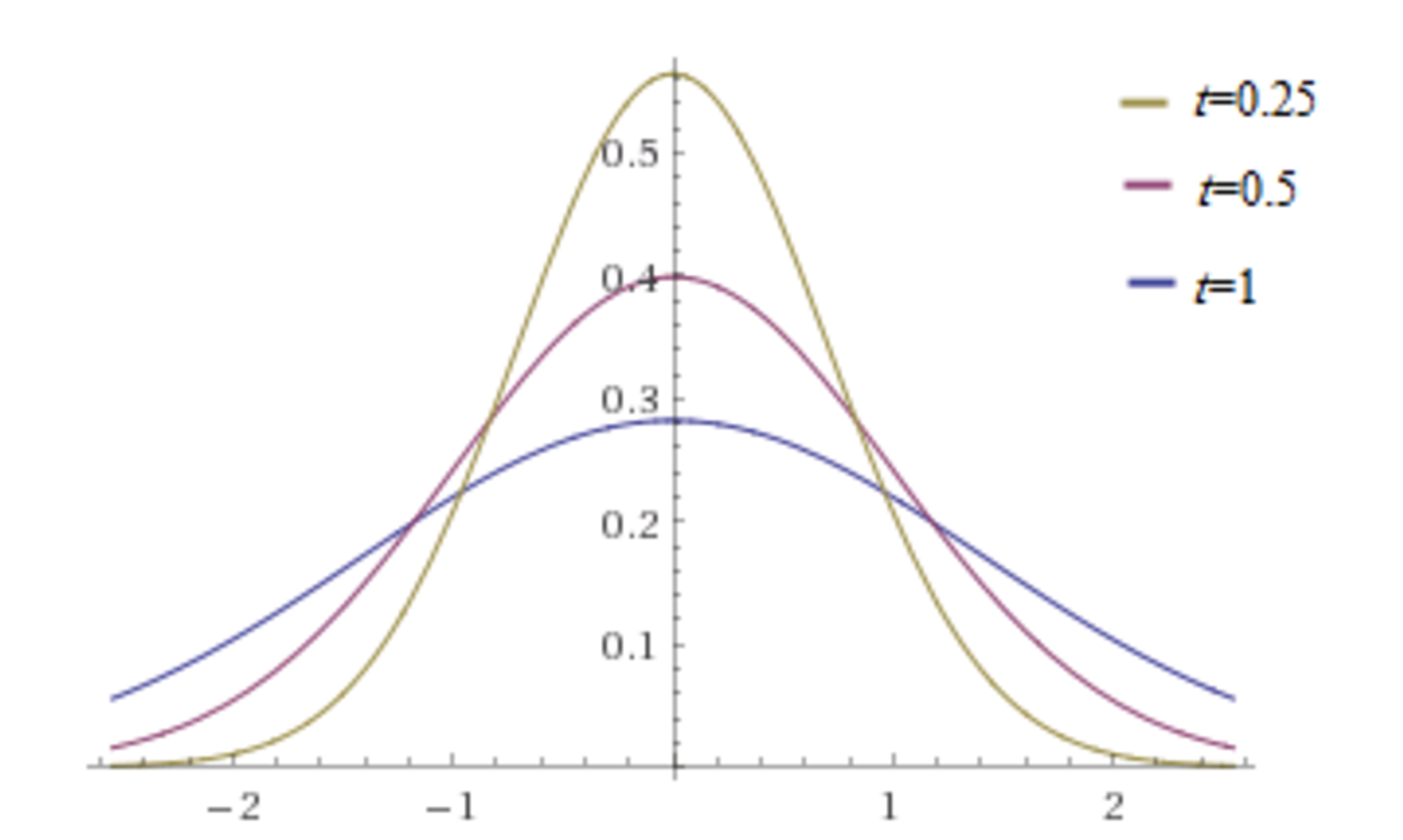
Simulatore online equazione calore. Sperimentando con i dati iniziali si puo` notare come anche dati iniziali irregolari, diventano istantaneamente differenziabili. Notare gli effetti diversi delle condizioni di contorno di Dirichlet e Neumann sulla soluzione di equilibrio raggiunta a tempi grandi.
-
Video sull'evoluzione equazione KdV con profilo iniziale cos(x) e condizioni di bordo periodiche. Si noti come nei primi istanti la soluzione evolve in modo simile all'equazione di Burgers inviscida, fino quasi a formare un fronte di shock. La soluzione pero` rimane a un sol valore, e si decompone in una sequenza di solitoni, che dominano la dinamica successiva. I solitoni interagiscono elasticamente e il loro numero non cambia.
-
Presentazione su equazione delle onde e musica all'universita` di Oxford.
-
Note da un corso universitario dell'universita` di McGill per chi volesse approfondire la fisica degli strumenti musicali.
-

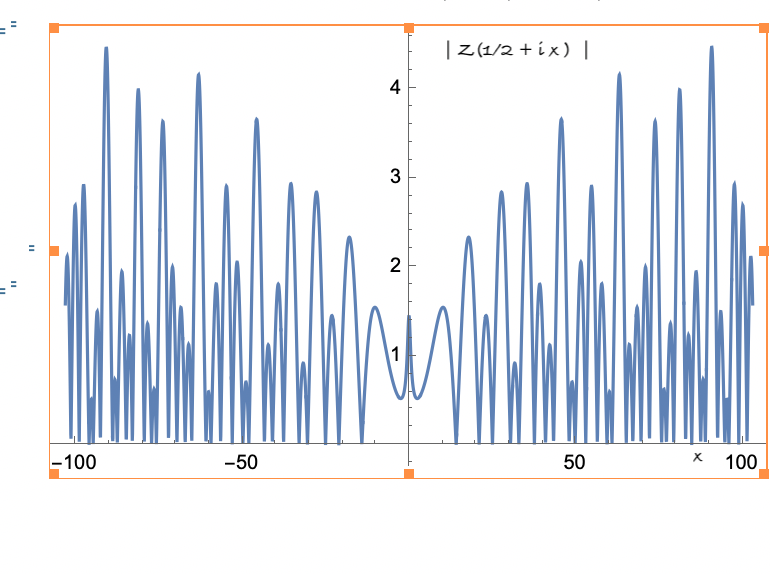
Il grafico mostra il valore assoluto della funzione Gamma di Eulero nel piano complesso.
-
-
Purtroppo per un problema tecnico e` stata registrata solo la prima parte della lezione 14. Gli argomenti trattati seguono comunque le note e sono reperibili registrazioni su questi argomenti su Moodle degli scorsi anni.







 Forma di una particolare soluzione dell'equazione differenziale ottenuta come superficie di livello del potenziale. Si noti che la funzione y(x) ha due rami distinti. Il punto in cui y'(x) = infinito e` un punto in cui non si applicano le condizioni del teorema di esistenza e unicita`.
Forma di una particolare soluzione dell'equazione differenziale ottenuta come superficie di livello del potenziale. Si noti che la funzione y(x) ha due rami distinti. Il punto in cui y'(x) = infinito e` un punto in cui non si applicano le condizioni del teorema di esistenza e unicita`. 

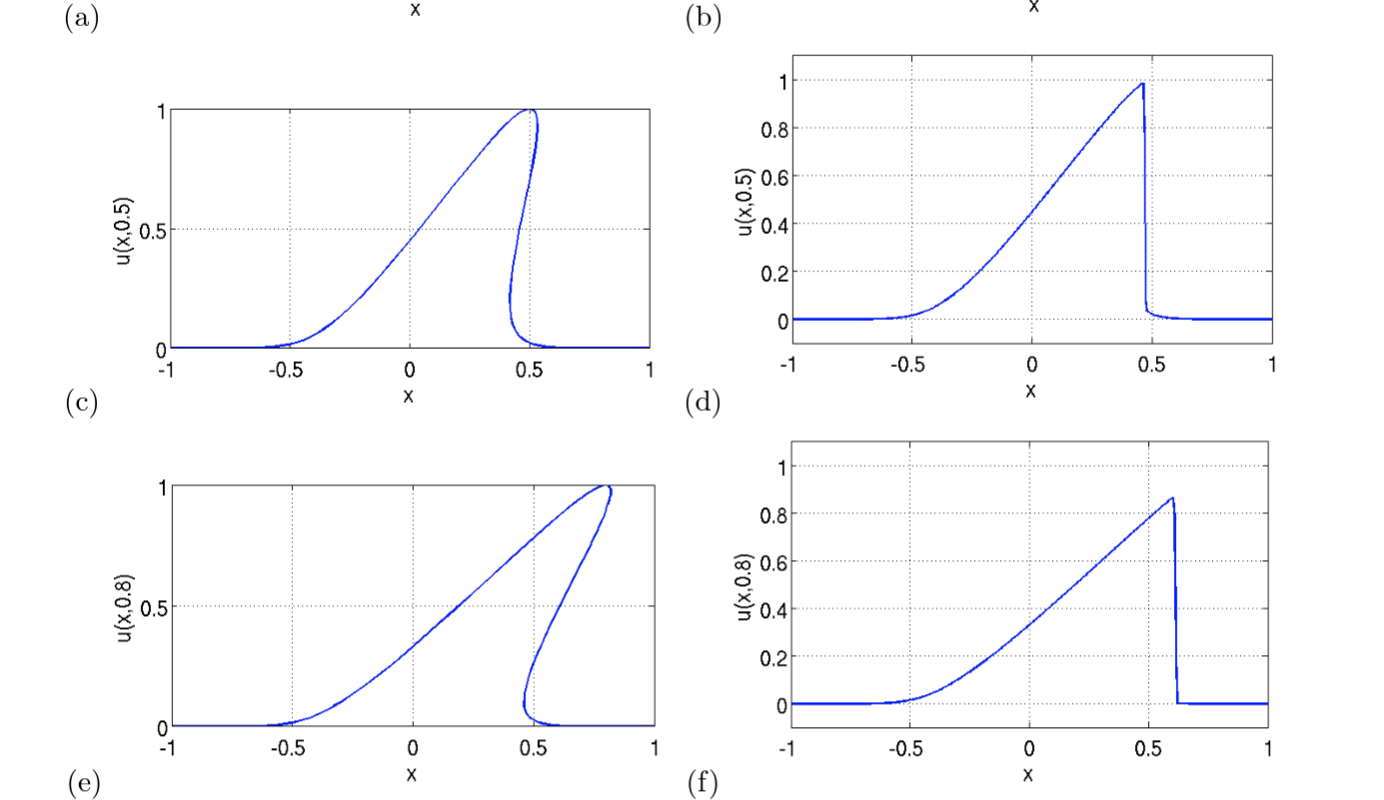
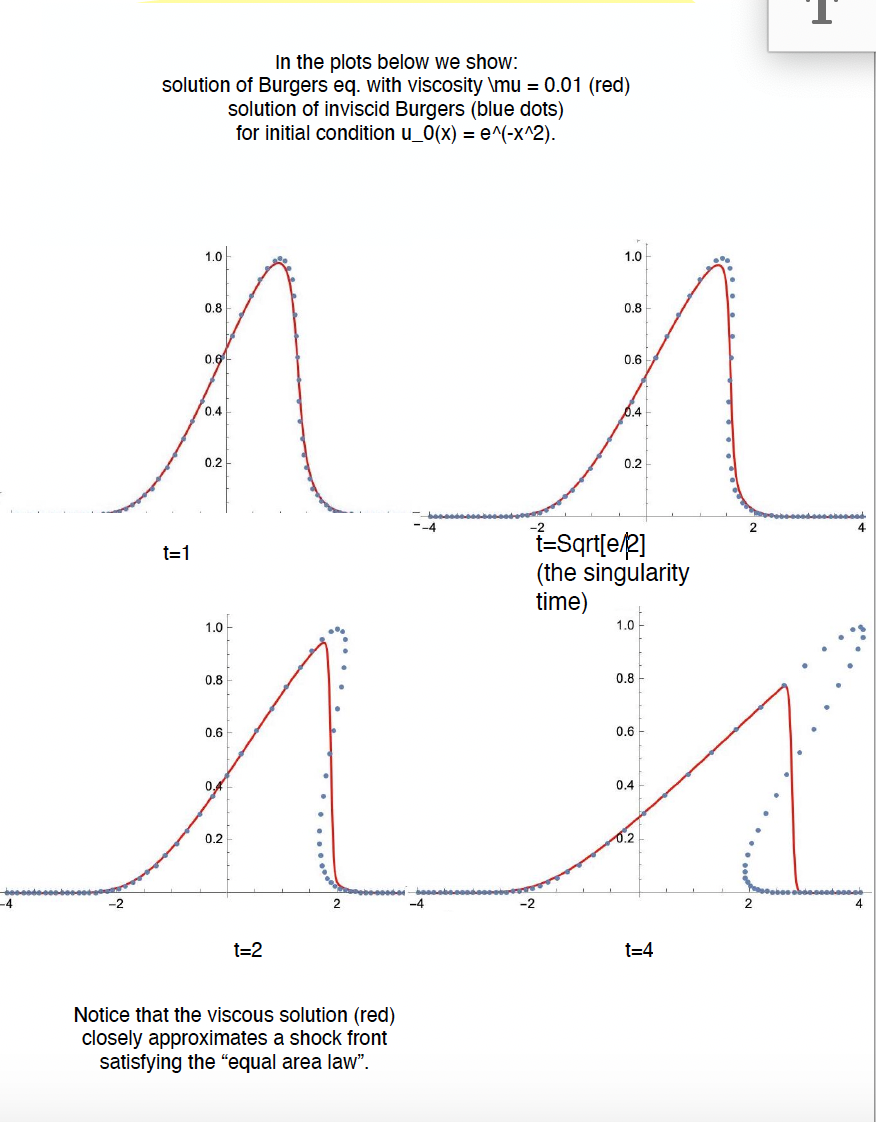
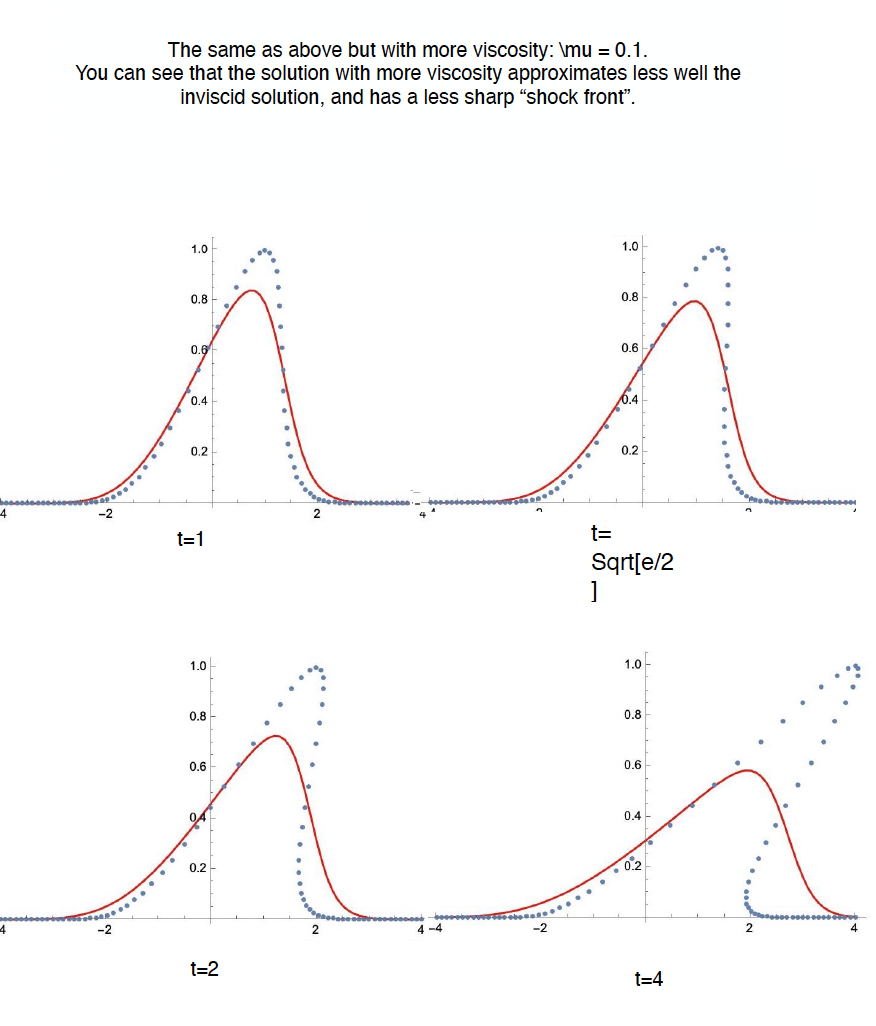
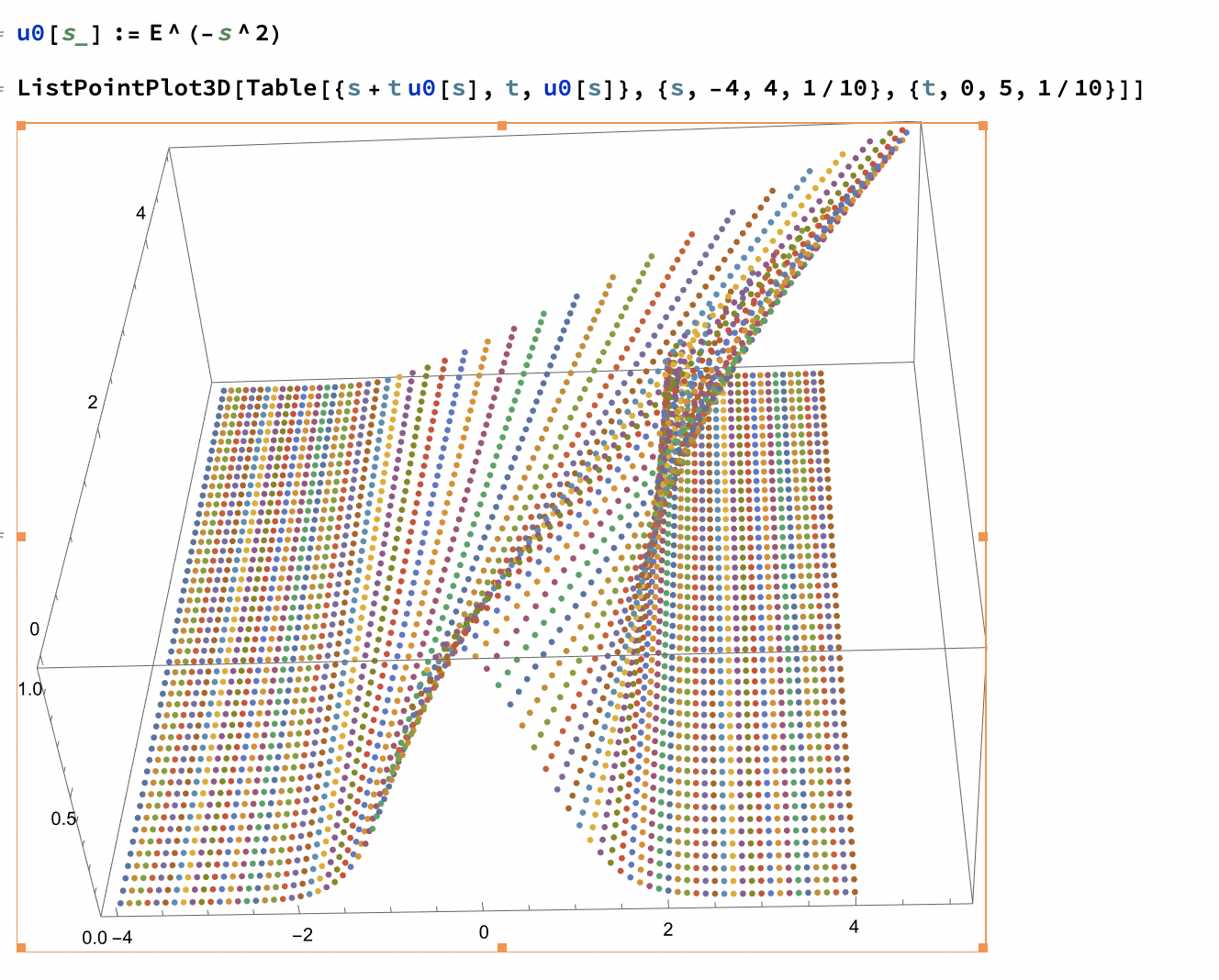 Fenomeno di formazione di una singolarita` per una soluzione dell'equazione di Burgers inviscida, con profilo iniziale gaussiano, risolta con il metodo delle caratteristiche. I semplici comandi in Mathematica illustrano come realizzare il grafico della soluzione a tempi generici. Sopo la formazione della singolarita` la soluzione diventa a piu` valori.
Fenomeno di formazione di una singolarita` per una soluzione dell'equazione di Burgers inviscida, con profilo iniziale gaussiano, risolta con il metodo delle caratteristiche. I semplici comandi in Mathematica illustrano come realizzare il grafico della soluzione a tempi generici. Sopo la formazione della singolarita` la soluzione diventa a piu` valori.