Schema della sezione

  • Minimizza Espandi

    Annunci

    Minimizza tutto Espandi tutto

    SOLUZIONI ESAMI PASSATI:

    Si segnala che nella sezione sulle prove d'esame sono state aggiunte le soluzioni delle prove di quest'anno. 

    APPELLI:

    Nella sessione di settembre ci saranno i seguenti appelli:

    - scritto: martedi` 10 settembre 14:00 - 16:00 , aula A
    - orale:  venerdi` 13 settembre , Aula Franzinetti, 9:00-13:00.


    • Per la sessione estiva le date degli esami saranno:

      - prova scritta I : 17/06/2024 14:00-16:00 Aula 304 Edificio "Ex La Stampa"

      - prova orale I :  20/06/2024 10:00 Aula Fubini

      - prova scritta II : 16/07/2024 10:00-12:00 Aula 304 Edificio "Ex La Stampa"

      - prova orale II : 18/07/2024 10:00 Aula Verde.


      Studenti e studentesse che avessero problemi di sovrapposizioni con altri esami sono invitat* a contattare il docente.


    • Informazioni sull'esame File
  • Minimizza Espandi

    Esercizi

  • Minimizza Espandi

    Note aggiornate

    • Questa sezione contiene le note aggiornate per l'anno in corso. 

    • Note aggiornate 1 - Funzioni speciali File
    • Note aggiornate 2 - ODE File

      Le principali differenze rispetto alle note degli anni precedenti sono due parti aggiuntive: metodo delle funzioni di Green (p. 28), e metodo dell'equilibrio dominante per espandere intorno a punti singolari irregolari (p. 99). 

    • Note aggiornate 3 - PDE 1st order File

      (solo piccole correzioni rispetto alle note dello scorso anno)

    • Note aggiornate 4 - PDEs 2nd order - onde, metodo Fourier, metodo autofunzioni in dimensione generica File

      (nota: la parte sulle armoniche sferiche non e` stata discussa a lezione ed e` un contenuto di approfondimento non richiesto per l'esame). 

    • Note aggiornate 5 - equazione calore File

      (rispetto alla versione dell'anno scorso solo piccole correzioni. La parte sul principio di massimo/minimo per l'equazione del calore non e` stata discussa a lezione ed e` una lettura di approfondimento non richiesta per l'esame). 

    • Note aggiornate 6 - equazioni di Laplace e Poisson File

      Solo piccole correzioni rispetto alle note dello scorso anno.

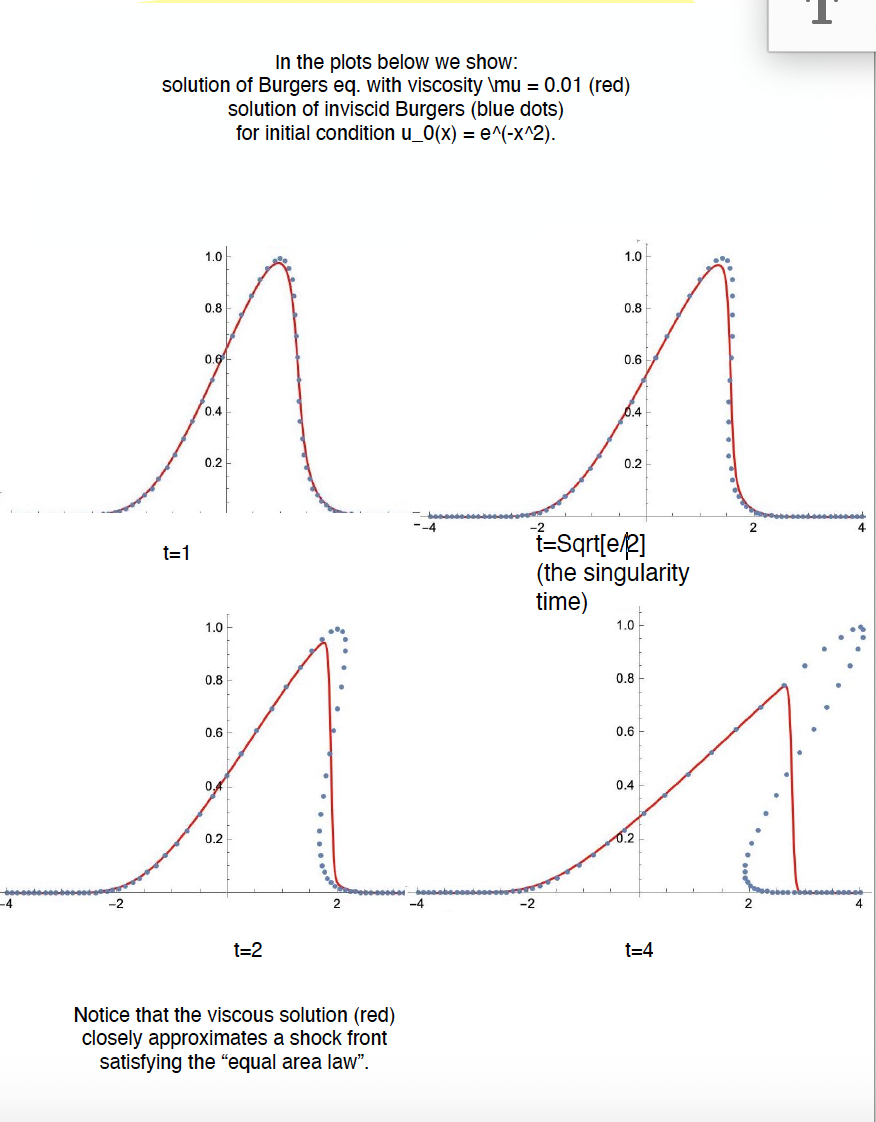
    • Note 7 - Burgers, shocks e viscosita` File

      Rispetto alle note dello scorso anno, e` stata aggiunta una discussione finale che mostra, considerando il metodo del punto a sella, il meccanismo con cui viene generato un fronte di shock nel limite di piccola viscosita`. 

    • [NOTA: la parte finale delle note dello scorso anno (parte 8 delle note 2022/2023, su complementi di analisi complessa) non e` stata trattata quest'anno, e non verra` richiesta all'esame. Per chi fosse curios*, le note corrispondenti si possono trovare in una sezione successiva di Moodle. ]

  • Minimizza Espandi

    Esempi di prove d'esame

  • Minimizza Espandi

    Note dello scorso anno 2022/2023

  • Minimizza Espandi

    Risorse per approfondimenti

    • Digital Library of Mathematical Functions URL
    • Why are special functions special? File
      Articolo del famoso fisico matematico Michael Berry
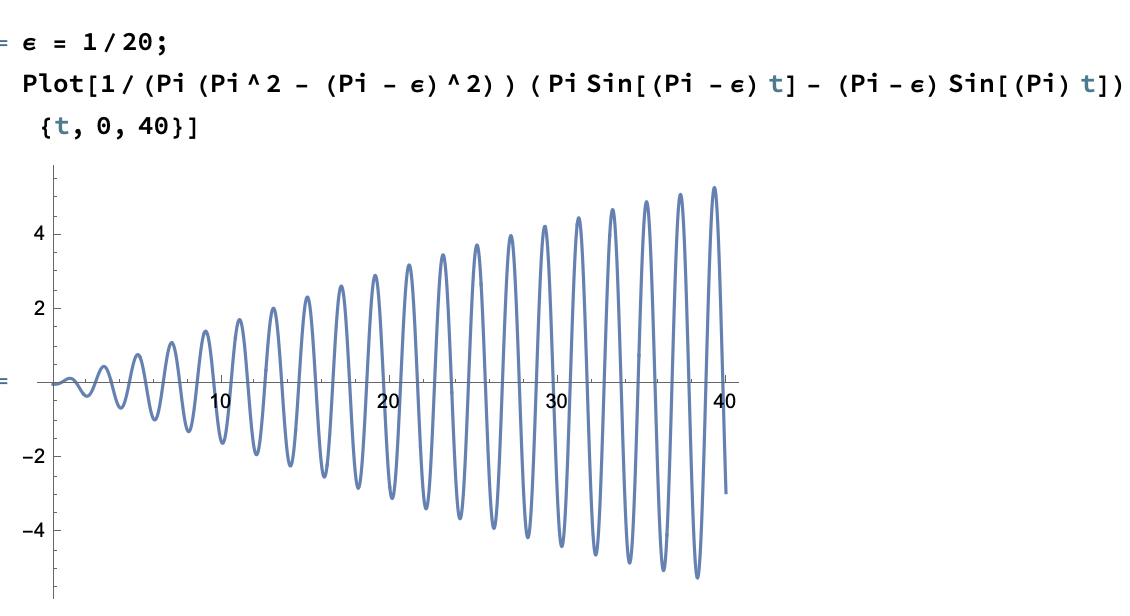
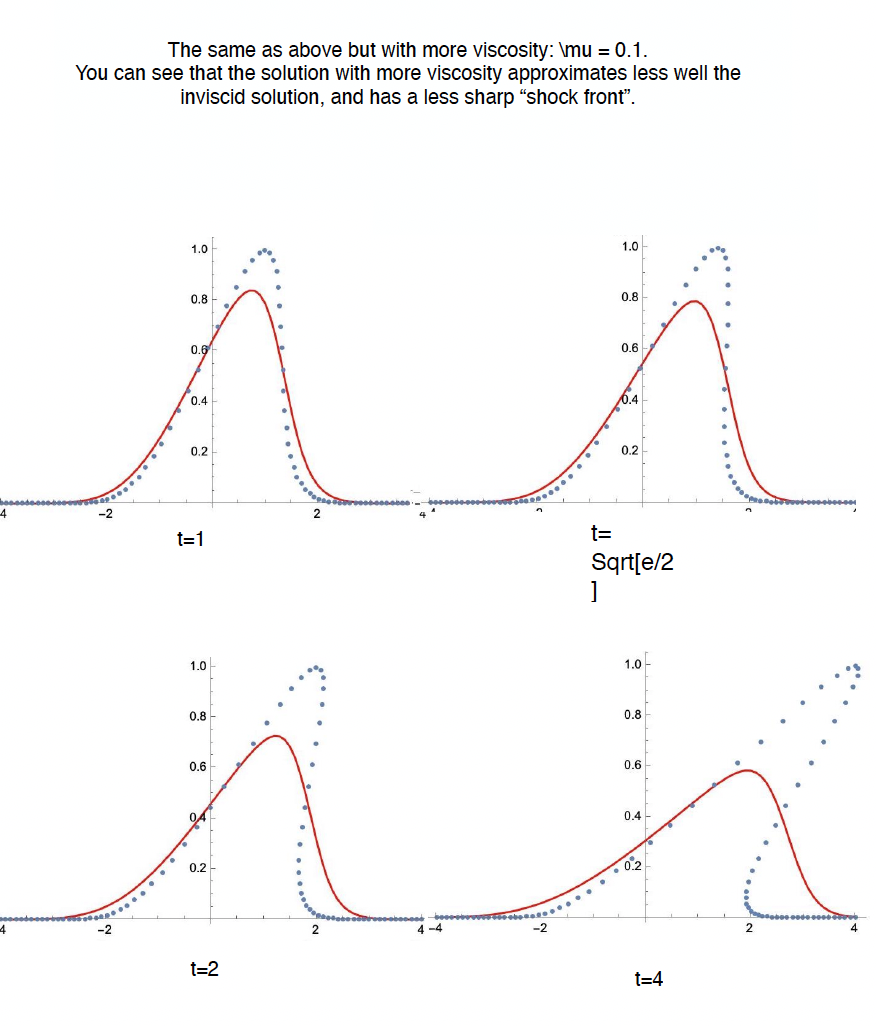
    • Teoria dell'arcobaleno di Airy (in cui la funzione di Airy vista a lezione descrive le frange sovranumerarie) URL
    • programma di calcolo simbolico per risolvere equazione di Burgers File

      Con un qualsiasi programma di calcolo simbolico (Maple, Mathematica, Python (open access), o molti altri), si puo` facilmente adattare il programma per generare una soluzione dell'equazione di Burgers con profilo iniziale a piacere. Il metodo si puo` generalizzare per risolvere nello stesso modo, con il metodo delle curve caratteristiche, qualsiasi PDE con derivate del prim'ordine. 

    • simulatore online equazione delle onde 1D URL
    • Simulatore online equazione calore URL

      Simulatore online equazione calore. Sperimentando con i dati iniziali si puo` notare come anche dati iniziali  irregolari, diventano istantaneamente differenziabili. Notare gli effetti diversi delle condizioni di contorno di Dirichlet e Neumann sulla soluzione di equilibrio raggiunta a tempi grandi. 

    • Video su comportamento equazione KdV e solitoni (discussi nella lezione 20). URL

      Video sull'evoluzione equazione KdV con profilo iniziale cos(x) e condizioni di bordo periodiche. Si noti come nei primi istanti la soluzione evolve in modo simile all'equazione di Burgers inviscida, fino quasi a formare un fronte di shock. La soluzione pero` rimane a un sol valore, e si decompone in una sequenza di solitoni, che dominano la dinamica successiva. I solitoni interagiscono elasticamente e il loro numero non cambia. 

    • Interactions of solitons in collisionless plasma File

      Un famoso e breve articolo in cui si descrive il primo studio dell'equazione di KdV e la scoperta dei solitoni. Lo studio descritto e` lo stesso illustrato nel video precedente.

    • Oscillatori nonlineari di Fermi-Pasta-Ulam-Tsingou URL
      Descrizione del primo esperimento numerico nella storia della fisica, il problema di Fermi-Pasta-Ulam-Tsingou,  i cui risultati iniziarono il campo di studio su equazioni nonlineari e portarono alla scoperta delle proprieta` particolari dell'equazione di KdV. 
    • Can you hear the shape of a drum? URL
    • Notes on Physics of Music File

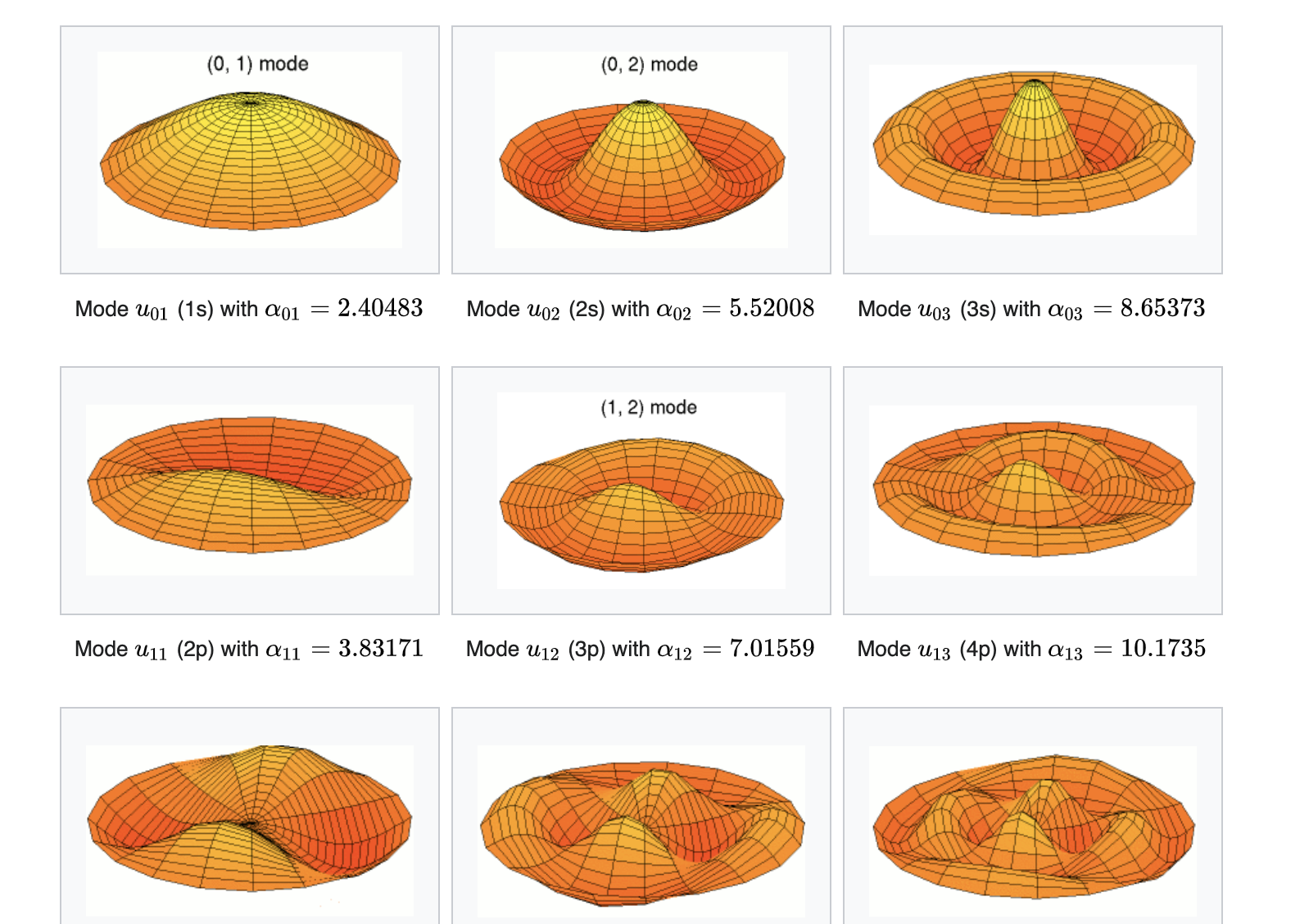
      Note da un corso universitario dell'universita` di McGill per chi volesse approfondire la fisica degli strumenti musicali.

  • Minimizza Espandi

    Lezione 1: introduzione alle funzioni speciali e funzione Gamma


    Il grafico mostra il valore assoluto della funzione Gamma di Eulero nel piano complesso.

    • Argomenti discussi:
      Introduzione alle funzioni speciali. 
      Funzione Gamma di Eulero: rappresentazione integrale e regione di validita` ; relazione di ricorrenza ; posizione dei poli della funzione Gamma ; relazione con il fattoriale dei numeri interi. 
      Il concetto di serie asintotica e le differenze dalle serie convergenti ordinarie. 
  • Minimizza Espandi

    Lezione 2: formula di Stirling e introduzione alla Zeta di Riemann

    • Argomenti trattati: 

      Derivazione della formula di Stirling usando il metodo del punto a sella, di cui abbiamo descritto il funzionamento in generale. (NOTA: nella lezione si usa notazione F(w), che corrisponde a -S(w) delle note).

      Formula di riflessione per la funzione Gamma e conseguenza: Gamma non ha zeri. 

      Funzione Beta di Eulero e legame con la Gamma di Eulero.

      Definizione funzioni Poligamma. 

      Inizio studio Zeta di Riemann; definizione come serie, dominio di convergenza. 

      Relazione con funzione Eta di Dirichlet che permette di estendere Zeta alla striscia critica.

    • Registrazione_parte_1 URL
    • registrazione_parte_2 URL
  • Minimizza Espandi

    Lezione 3: proprieta` della Zeta di Riemann.

    • registrazione lezione 3 URL

    • Argomenti trattati: 

      formula di riflessione per la Zeta di Riemann, le sue conseguenze per la posizione di poli e zeri. Ipotesi di Riemann sulla posizione degli zeri non triviali della funzione.

      Legame con i numeri primi attraverso la rappresentazione di Zeta come prodotto infinito. 

      La rappresentazione integrale di Zeta e il legame con la distribuzione di Bose-Einstein.

      Definizione delle funzioni polilogaritmi. 

      Definizione delle funzioni ipergeometriche generalizzate.  

    • Zeri della zeta di Riemann sulla linea critica

      Il grafico del modulo della Zeta di Riemann sulla linea critica, con visibili alcuni degli zeri descritti dall'ipotesi di Riemann (che dice che tutti gli zeri, a parte quelli triviali, si trovano sulla linea critica). La posizione di questi zeri non e` regolare. 


    • Nella figura sono illustrate le proprieta` principali della Zeta di Riemann.


    • La funzione che conta i numeri primi. Attraverso il legame tra numeri primi e Zeta di Riemann si riesce a stabilire il comportamento per grande argomento della funzione (quindi informazione sulla distribuzione asintotica dei numeri primi). 

  • Minimizza Espandi

    Lezione 4: funzioni ipergeometriche generalizzate, e introduzione alle equazioni differenziali ordinarie.

    • registrazione lezione 4 URL

    • Argomenti trattati:

      fine discussione delle funzioni ipergeometriche generalizzate.  Criteri per la convergenza dell'espansione in serie, e definizione della funzione ipergeometrica di Gauss. 

      Discussione di alcune proprieta` generali di equazioni differenziali ordinarie, e alcuni tipi di equazioni differenziali esattamente risolubili: in particolare equazioni separabili e equazioni in forma di differenziale esatto. 

      Equazioni lineari: definizione del Wronskiano per verificare se n soluzioni  sono linearmente indipendenti. 

  • Minimizza Espandi

    Lezione 5: proprieta` di equazioni differenziali lineari.

    • registrazione lezione 5 URL

    • Argomenti trattati: 

      Metodo di variazione delle costanti per costruire soluzioni extra di equazioni differenziali lineari, omogenee o inomogenee. 

      Metodo della funzione di Green per costruire soluzioni di un'equazione differenziale lineare inomogenea, data una base di soluzioni dell'equazione omogenea. 

      Abbiamo illustrato il caso di equazione del prim'ordine, e discusso i risultati nel caso di equazione del second'ordine. 

      Abbiamo discusso la derivazione dell'equazione differenziale per il Wronskiano di un'equazione differenziale del second'ordine. 

  • Minimizza Espandi

    Lezione 6: Metodi di soluzione per serie in punti regolari e singolari fuchsiani.

    • registrazione parziale lezione 6 URL

      Purtroppo parte della seconda ora di lezione non e` stata registrata per errore. Gli argomenti trattati sono gli stessi della lezione 5 dello scorso anno. 

    • Argomenti trattati: 

      punti regolari, singolari regolari (fuchsiani) e singolari irregolari di equazioni differenziali lineari. 

      Abbiamo svolto l'esempio di calcolo per serie della soluzione dell'equazione di Airy con generica condizione iniziale in x=0, riscritta in termini di funzioni ipergeometriche generalizzate. 

      (Abbiamo fatto cenni al ruolo di una delle due funzioni di Airy nella teoria dell'arcobaleno.)  


    • Funzione di Airy



    • Seconda funzione di Airy, detta Bi(x), soluzione indipendente dell'equazione differenziale.


    • La prima funzione di Airy descrive l'interferenza tra i raggi prossimi al raggio di maggior focalizzazione (raggio caustico).


    • ... e modellizza la posizione angolare degli archi sovranumerari visibili nella figura sotto l'arco principale. 

  • Minimizza Espandi

    Lezione 7. Equazioni con 3 singolarita` fuchsiane: il metodo di Papperitz-Riemann

    • registrazione lezione 7 URL

    • Abbiamo studiato il metodo del simbolo "P", per risolvere le equazioni lineari del II ordine, con solo 3 singolarita`  tutte fuchsiane. 

      Abbiamo studiato la forma semplificata che un'equazione con tre singolarita`  fuchsiane assume grazie al teorema di Liouville di analisi complessa. 

      Simbolo P, e sua forma canonica che si ricollega all'eq. differenziale ipergeometrica di Gauss. 

      Trasformazioni del simbolo P sotto trasformazioni conformi del piano complesso esteso (trasformazioni lineari fratte), e sotto ridefinizione degli indici. 

      Abbiamo usato queste trasformazioni per costruire una base di soluzioni dell'equazione ipergeometrica intorno a x=0, e una seconda base costruita intorno a x=1. 



    • Illustrazione gemetrica di una trasformazione lineare fratta (mappa conforme): una mappa che preserva gli angoli ma non le distanze. Le trasformazioni conformi si possono incontrare in ogni dimensione, non solo in due dimensioni come nel nostro caso. L'invarianza  sotto trasformazioni conformi emerge in molti modelli fisici nel punto in cui avvengono transizioni di fase del second'ordine. Al punto critico in cui due fasi  (ad esempio, le fasi liquido-vapore) si toccano in modo continuo, le osservabili del sistema sono invarianti sotto ridefinizione della scala delle lunghezze. Questa invarianza di scala spesso implica anche l'invarianza sotto le piu` generali trasformazioni conformi della geometria del sistema. 

  • Minimizza Espandi

    Lezione 8: Espansione asintotica intorno a singolarita` irregolari.

    • Abbiamo studiato il metodo dell'equilibrio dominante per derivare un'espansione asintotica intorno a punti singolari non fuchsiani di un'equazione differenziale lineare.

      Un esempio che abbiamo studiato riguarda l'espansione per grande argomento delle soluzioni dell'equazione di Airy.  

    • registrazione lezione 8 URL
  • Minimizza Espandi

    Lezione 9. Metodi perturbativi per equazioni ordinarie, e inizio equazioni alle derivate parziali.

  • Minimizza Espandi

    Lezione 10: Curve caratteristiche per PDE lineari

  • Minimizza Espandi

    Lezione 11. Curve caratteristiche in PDE quasilineari, equazione di Burgers e fenomeno di formazione di uno shock

    • registrazione lezione 11 URL

    • Argomenti trattati a lezione: 

      Abbiamo descritto come funziona il metodo delle caratteristiche per equazioni quasi-lineari. 

      Abbiamo parlato del problema di Cauchy con condizioni iniziali su una curva nel piano (x,y), e delle condizioni affinche` il problema abbia una soluzione unica in un intorno della curva iniziale. 

      Abbiamo studiato la soluzione con il metodo delle caratteristiche dell'equazione di Burgers inviscida, e descritto come la soluzione, anche se i dati iniziali sono regolari, puo` sviluppare delle singolarita` con l'evoluzione temporale. Le singolarita` si manifestano con la creazione di uno shock (un punto con gradiente infinito), e a tempi successivi la soluzione diventa a piu` valori. Abbiamo spiegato come questo sia dovuto all'incrociarsi di diverse curve caratteristiche. Abbiamo ricavato un'equazione che descrive quando si forma la singolarita`, in termini delle variabili che parametrizzano le curve caratteristiche. L'equazione verra` usata nella prossima lezione per calcolare il tempo in cui si forma uno shock, data una condizione iniziale generica. 


    • Una soluzione dell'equazione di Burgers inviscida. La soluzione parte con un profilo regolare a t=0, sviluppa un gradiente infinito a un certo istante, e successivamente diventa una funzione a piu` valori. Il grafico e` ottenuto con il metodo delle caratteristiche discusso a lezione. Il codice usato per produrre il grafico e` allegato in pdf. 

    • codice per soluzione equazione di Burgers File

      Il codice permette di produrre il grafico della soluzione, dato un certo profilo iniziale, usando il metodo delle caratteristiche, in particolare usa la soluzione per le curve caratteristiche vista a lezione. (Il programma e` scitto in Mathematica, ma si puo` facilmente adattare a altri  programmi di calcolo simbolico, ad esempio Python che e` open access).

  • Minimizza Espandi

    Lezione 12. Soluzioni deboli dell'equazione di Burgers e metodo delle caratteristiche per equazioni nonlineari

    • registrazione lezione URL

    • Argomenti trattati a lezione:

      Abbiamo discusso la derivazione dell'equazione di Burgers (senza viscosita`) come modello semplificato delle equazioni di Eulero della fluidodinamica in una dimensione. 

      Abbiamo descritto intuitivamente il concetto di soluzioni deboli, come soluzioni che possono avere discontinuita`  che modellizzano il fronte di shock per istanti successivi alla formazione della singolarita`, in modo da rendere la soluzione a un sol valore. (Le note su questa parte si trovano verso la fine delle note dello scorso anno, nel capitolo su Burgers con viscosita`). Come criterio fisico per stabilire la posizione del fronte di shock, abbiamo descritto l'interpretazione dell'equazione come legge di conservazione: la forma integrale della legge di conservazione ci permette di considerare non solo soluzioni differenziabili, ma anche soluzioni con un fronte di shock, e impone una relazione che determina la velocita` del fronte di shock: la condizione di  Rankine-Hugoniot. 

      Siamo poi tornati al metodo delle caratteristiche, spiegando come funziona nel caso pienamente nonlineare. 

      Abbiamo iniziato a considerare l'equazione eikonale u_x^2 + u_y^2 = 1 , in particolare il problema ai valori iniziali in cui u = 1 sulla circonferenza x^2 + y^2 = 1. 

  • Minimizza Espandi

    Lezione 13: Esercitazione su equazioni differenziali ordinarie

    • Esercitazione URL

    • Abbiamo risolto il problema n. 3 sul metodo di Papperitz-Riemann, e l'esercizio n. 1 sui punti irregolari (sull'espansione attorno a x->+infinito delle soluzioni dell'equazione di Bessel). 

      Alla fine della lezione sono stati proposti come esercizi l'espansione intorno a x->+infinito dell'equazione y'' = x^3 y , e l'esercizio n. 2.1 sui punti irregolari. In quest'ultimo  si dovrebbero trovare due possibili equilibri dominanti, entrambi consistenti, che corrispondono a due soluzioni con comportamento molto diverso per x->0^+: una soluzione che tende a una costante, e una con un comportamento divergente esponenzialmente. 

      Un altro esercizio interessante e` il n. 2.2, che presenta un caso in cui S''>>(S')^2  invece che S''<<(S')^2. 

  • Minimizza Espandi

    Lezione 14: equazione eikonale e inizio equazione delle onde

    • registrazione parte 1 URL
    • registrazione parte 2 URL

    • Abbiamo finito di svolgere un esercizio sull'equazione eikonale con il metodo delle caratteristiche per equazioni completamente nonlineari di ordine 1. Abbiamo discusso l'interpretazione dell'equazione eikonale nell'ambito della propagazione di luce monocromatica in un mezzo, e discusso la sua relazione con l'ottica geometrica in cui i raggi di luce si muovono lungo le curve caratteristiche. 

      Abbiamo poi iniziato il capitolo sulle PDE lineari del second'ordine. Abbiamo dicusso brevemente la classificazione delle equazioni in due variabili in iperboliche, paraboliche e ellittiche. 

      Abbiamo poi iniziato a discutere l'equazione delle onde, derivando la soluzione del problema di Cauchy sulla linea infinita nel caso di propagazione di onde in una dimensione (formula di d'Alembert). 

      Nella sezione approfondimenti si trova un simulatore di soluzioni dell'equazione delle onde. Alla fine della lezione abbiamo guardato alcuni esempi di soluzioni. 

  • Minimizza Espandi

    Lezione 15: equazione delle onde con bordi omogenei e metodo delle immagini.

    • registrazione URL

    • Abbiamo studiato la soluzione generale dell'equazione delle onde con un termine forzante inomogeneo su una linea infinita. Abbiamo discusso la soluzione per il problema ai valori iniziali per l'equazione delle onde in spazio infinito, dato dalle formule di Kirchoff (scritte verso la fine delle note degli scorsi anni), e fatto alcuni commenti sulla differenza tra il comportamento dell'equazione delle onde in dimensione 2 e 3 : in 3 dimensioni i suoni hanno durata finita, mentre in 2 dimensioni hanno durata infinita. 

      Siamo poi tornati in dimensione D=1, e abbiamo iniziato a considerare condizioni di bordo, di Dirichlet o Neumann, per l'equazione delle onde: abbiamo mostrato come il problema puo` essere esaminato usando il metodo delle immagini, che permette di mappare il problema su un problema sulla linea infinita, ma con condizioni iniziali estese in modo opportuno sul resto della linea. 

      Per condizioni di bordo non omogenee, sara` necessario usare il metodo molto piu` potente noto come metodo di Fourier o metodo di espansione in autofunzioni, che vedremo la prossima settimana e, opportunamente generalizzato, ci aiutera` anche a risolvere le equazioni delle onde, del calore e di Laplace in dimensione piu` alta. 

  • Minimizza Espandi

    Lezione 16: metodo di Fourier

    • registrazione lezione URL

    • Abbiamo trattato il metodo di decomposizione in serie di Fourier per risolvere l'equazione delle onde in una dimensione spaziale, considerando il problema di Cauchy su un intervallo con condizioni di bordo di Dirichlet o Neumann (possibilmente diverse ai due estremi dell'intervallo). 

      Abbiamo iniziato a discutere come trattare condizioni di bordo non omogenee, senza ancora trattare in dettaglio il caso dipendente dal tempo. 

      Gli ultimi 10 minuti di lezione trattano in modo informale un'introduzione alla connessione tra armoniche su una corda e note musicali (questa parte e` stata trattata solo rapidamente e non verra` esaminata). 

  • Minimizza Espandi

    Lezione 17: esercitazione su metodo caratteristiche

    • NOTA: le soluzioni degli esercizi sono state caricate nella sezione Esercizi di Moodle.
    • registrazione lezione URL

    • Abbiamo risolto in dettaglio gli esercizi 3,4,5, e discusso il metodo per risolvere l'esercizio 6 impostando l'inizio della soluzione, in particolare come calcolare le quantita` u_x, u_y sulla curva delle condizioni iniziali (queste quantita` servono successivamente come condizioni iniziali per le equazioni delle curve caratteristiche). 

      Negli ultimi minuti della lezione abbiamo commentato, non in dettaglio, alcuni grafici generati con il metodo delle curve caratteristiche per la soluzione di alcuni degli esercizi. 

      I grafici sono visualizzabili sul pdf caricato in questa sezione. 

    • ILLUSTRAZIONI soluzioni File
  • Minimizza Espandi

    Lezione 18: fenomeno della risonanza e inizio equazione del calore

    • registrazione lezione URL

      Purtroppo parte della registrazione e` andata persa perche` e`  mancata l'alimentazione del computer dell'aula. 



    • Un'illustrazione del segnale amplificato generato da un termine forzante con una frequenza vicina a una delle frequenze tipiche del sistema (fenomeno della risonanza). 

    • Abbiamo discusso come risolvere l'equazione delle onde con condizioni di bordo non omogenee dipendenti dal tempo, riconducendoci alla soluzione di un problema inomogeneo associato. 

      Abbiamo discusso la soluzione generale dell'equazione delle onde inomogenea su un intervallo con il metodo di Fourier.  Esaminando la soluzione, abbiamo discusso il fenomeno della risonanza. 

      I metodi discussi per trattare condizioni di bordo inomogenee e equazioni inomogenee si possono applicare anche per risolvere altri problemi, come quelli legati all'equazione del calore. 

      Abbiamo iniziato a discutere le proprieta` dell'equazione del calore. Abbiamo discusso le proprieta` di alcune soluzioni numeriche usando un simulatore numerico dell'equazione (link nella sezione approfondimenti di Moodle). 

      Abbiamo infine discusso una derivazione dell'equazione a partire dalla legge di Fourier per la conduzione del calore. 


  • Minimizza Espandi

    Lezione 19: soluzioni equazione del calore

    • Soluzioni eq. calore File

    • Abbiamo discusso come risolvere l'equazione del calore sia su spazio infinito, che su un intervallo nel caso unidimensionale con il metodo di Fourier. 

      Nel caso infinito, in dimensione generica, abbiamo derivato la soluzione del problema di Cauchy in termine di una convoluzione con l' "heat kernel", che fornisce la soluzione dell'equazione del calore con una condizione iniziale data da una delta di Dirac. Inoltre abbiamo discusso come scrivere la soluzione dell'equazione del calore inomogenea sulla linea infinita, usando il metodo della funzione di Green. 

      Abbiamo discusso di come trovare la soluzione di problemi di bordo su un intervallo, e l'interpretazione fisica di diverse condizioni di bordo: bordi isolati corrispondono a condizioni di bordo omogenee di Neumann, e bordi mantenuti a temperatura fissata danno luogo a condizioni di bordo di Dirichlet. 

      Abbiamo commentato i grafici di alcune soluzioni ottenute con questo metodo, si veda il file pdf allegato.

       Nella sezione esercizi sono stati caricati esercizi su PDE del 2nd ordine, tra cui alcuni sull'equazione del calore.

    • registrazione lezione URL
  • Minimizza Espandi

    Lezione 20 - equazione di Burgers con viscosita` e inizio PDE in D>1.

    • registrazione parte 1 URL

      Purtroppo ci sono stati dei problemi tecnici nella registrazione di alcune parti della prima parte della lezione. Gli appunti corrispondenti si trovano nella parte delle note sull'equazione di Burgers con viscosita` (verso la fine delle note dello scorso anno).

      Le altre parti registrate si trovano ai link: 

      - https://unito.webex.com/recordingservice/sites/unito/recording/f8385b0a7677103caffbbe32b373da81/playback

      - Seconda parte della lezione:  https://unito.webex.com/recordingservice/sites/unito/recording/f8385b0a7677103caffbbe32b373da81/playback

    • registrazione parte 2 URL
    • registrazione parte 3 URL




    • Abbiamo discusso come risolvere esplicitamente l'equazione di Burgers con un termine di viscosita`, tramite una mappa su soluzioni dell'equazione del calore che abbiamo risolto esplicitamente con il metodo dell' "heat kernel".  La soluzione ha una forma integrale, e abbiamo notato che il limite di piccola viscosita` di questa soluzione si puo` trattare con il metodo del punto a sella. Studiando questo limite abbiamo discusso come l'equazione con piccola viscosita` approssima la soluzione con fronti di shock discontinui (si vedano figure sopra), con la posizione degli shock definita in modo da tagliare porzioni di area uguale della soluzione. Tale definizione corrisponde a quella che avevamo discusso in precedenza interpretando l'equazione di Burgers come legge di conservazione. 

      Abbiamo poi fatto alcuni commenti sul comportamento di un'equazione con termine sia nonlineare che dispersivo (derivata cubica): l'equazione di KdV. Il comportamento di questa equazione e il fenomeno delle eccitazioni solitoniche si puo` visualizzare nel video allegato. 

      Infine, abbiamo iniziato a capire come risolvere PDE lineari su domini dati da una direzione temporale e uno spazio compatto in dimensione generica, con condizioni di bordo di Dirichlet o Neumann. Con in mente i casi dell'equazione delle onde e dell'equazione del calore, abbiamo delineato come usare il metodo di decomposizione in autofunzioni: la parte spaziale soddisfa l'equazione di Helmoltz, mentre la parte temporale soddisfa la stessa equazione di evoluzione temporale che nel caso unidimensionale.  


    • video evoluzione equazione di KdV URL
  • Minimizza Espandi

    Lezione 21 - Decomposizione in autofunzioni in D>1

    • Registrazione lezione URL

    • Abbiamo descritto come studiare l'equazione di Helmoltz nel caso di domini paerticolarmente semplici: nel caso di dominio rettangolare (che si generalizzano a parallelepipedi) con le serie di Fourier in piu` variabili, e nel caso del domnio dato dall'inerno di un disco con la decomposizione in funzioni funzioni di Bessel (anche dette funzioni cilindriche).

      Abbiamo commentato il fatto che le frequenze di oscillazioni dei tamburi ideali di forma circolare o rettangolare non sono commensurabili l'una all'altra: quindi le oscillazioni non sono periodiche nel tempo, a meno che si riesca a eccitare un solo modo. Questo e` il motivo per cui un tamburo di solito produce un "rumore" invece che un suono di altezza (cioe` frequenza) definita. 

      Abbiamo discusso la soluzione della parte radiale dell'equazione di Helmoltz all'interno di una sfera 3D assumendo che non ci sia dipendenza dalle coordinate angolari. Abbiamo presentato quindi il seguente problema, che verra` discusso venerdi`: studiare il problema di raffreddamento di una sfera solida che si trova inizialmente a temperatura uniforme T>0, e che e` immersa in uno spazio esterna di temperatura 0 (quindi si puo` assumere che la superficie esterna della sfera venga tenuta a temperatura =0). 


  • Minimizza Espandi

    Lezione 22 - Esercitazione

    • registrazione URL

    • Abbiamo discusso il problema del raffreddamento di una sfera, e alcuni esercizi sull'equazione del calore e delle onde trattati con il metodo di decomposizione in autofunzioni, discutendo gli esercizi 1,3,4,e in linee generali 6 e 7. 

  • Minimizza Espandi

    Lezione 23 - equazione di Laplace e Poisson

    • registrazione pt 1 (short) URL
    • registrazione pt2 URL
    • Equazioni di Laplace e Poisson. Principali applicazioni fisiche. Alcune proprieta` matematiche: differenziabilita` delle soluzioni, principio di massimo e minimo, principio della media. Legame con le funzioni olomorfe nel caso bidimensionale. Problemi matematici ben posti per queste equazioni e differenze con il caso dell'equazione delle onde e del calore. Soluzione dell'equazione di Poisson in spazio infinito con il metodo delle funzioni di Green. Formulazione della soluzione con funzione di Green nel caso di dominio generico. Inizio discussione del caso di spazio semi-infinito, in cui la funzione di Green appropriata si puo` costruire con il metodo delle immagini. 
  • Minimizza Espandi

    Lezione 24 - Laplace con il metodo di Fourier

    • registrazione lezione URL

    • Abbiamo finito di discutere il problema della soluzione dell'equazione di Laplace in un semipiano e discusso la soluzione dell'equazione di Laplace (problema di Dirichlet( in vari domini con simmetrie particolari che permettano di usare il metodo di decomposizione in autofunzioni. Abbiamo brevemente illustrato l'uso delle mappe tra funzioni olomorfe per risolvere l'equazione di Laplace in un dominio generico nel piano. Senza discutere i dettagli formali, questo e` stato illustrato con un esempio della mappa tra il problema di Neumann all'esterno di un cerchio e all'esterno di un dominio ellittico. 






    • file usato per generare i grafici delle linee di flusso intorno a ostacolo circolare e ellittico

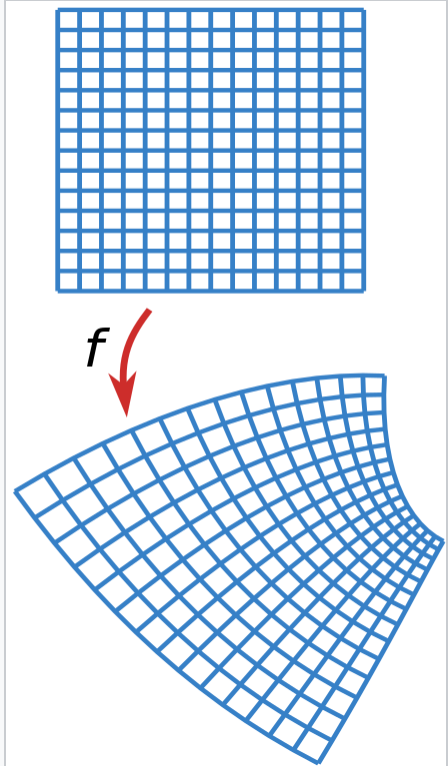
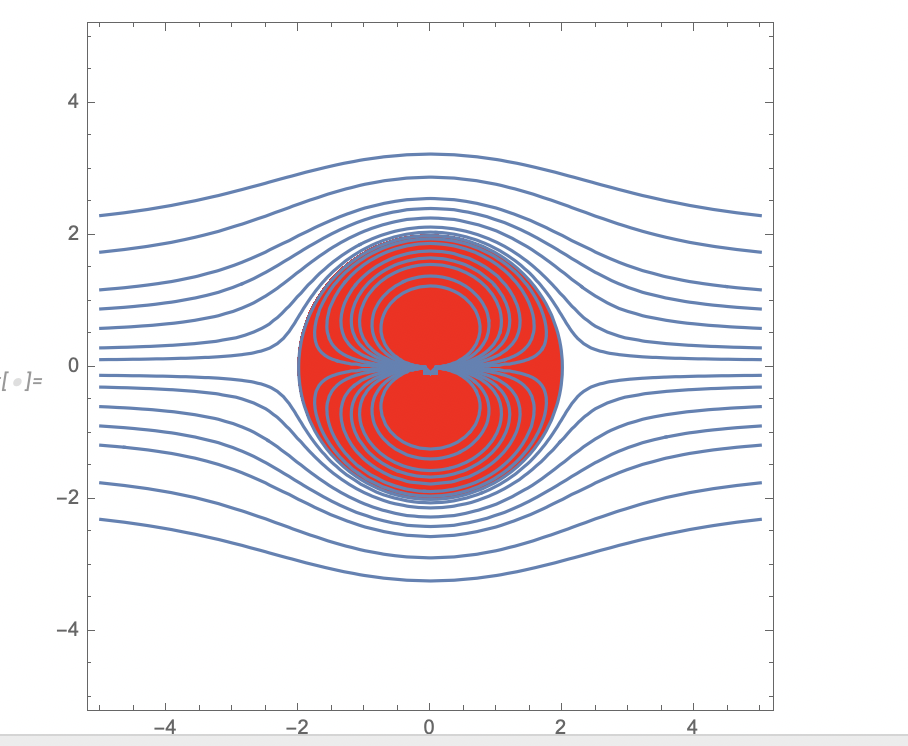
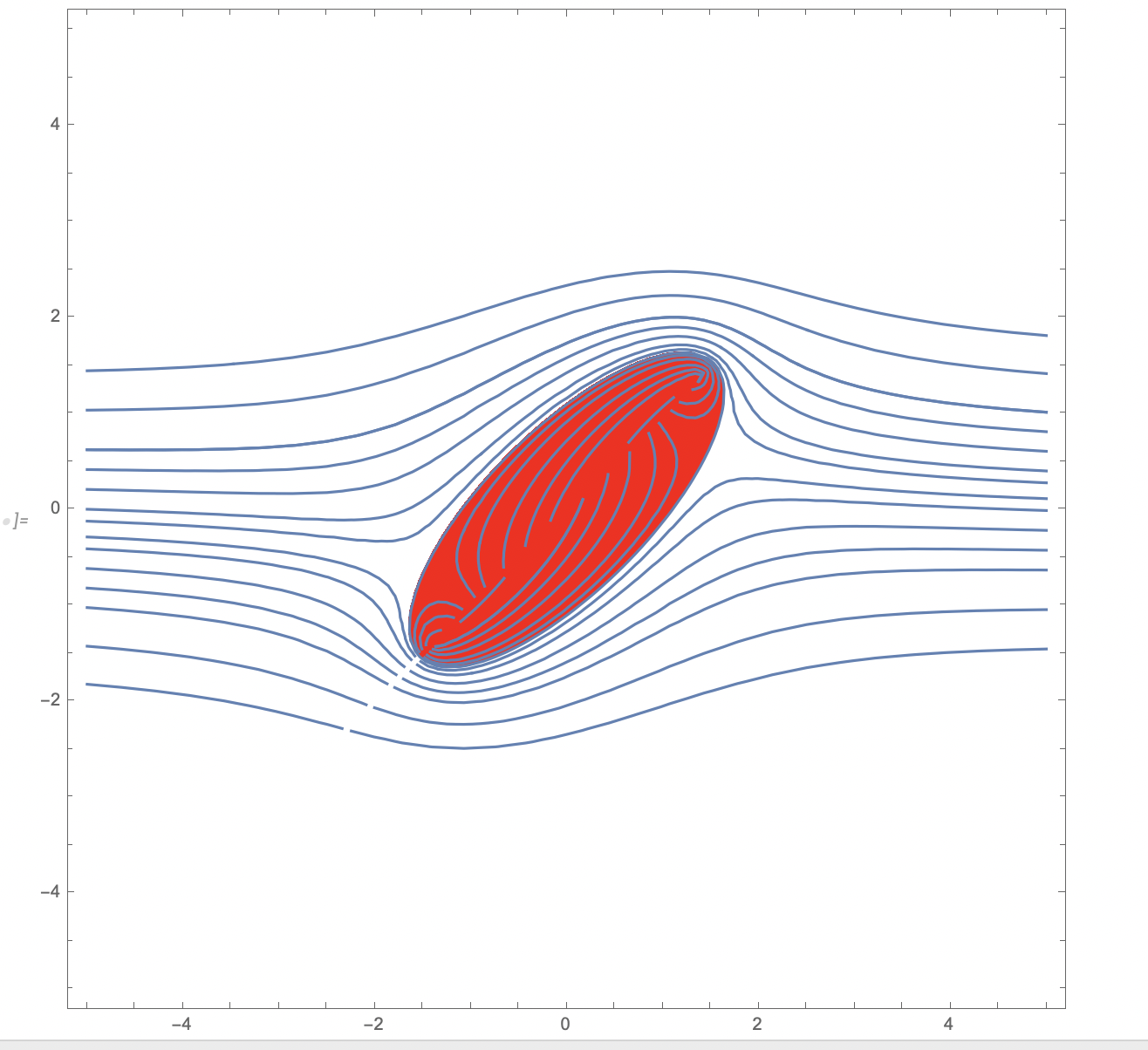
      I dettagli matematici della mappa conforme usata non sono importanti per l'esame. Le osservazioni importanti sono che le linee di flusso (parallele al gradiente del potenziale del flusso) sono ottenute come curve di livello della parte immaginaria della funzione complessa associata, dove la parte reale rappresenta il potenziale del flusso. Inoltre e` importante la comprensione del principio generale per cui facendo una composizione di mappa olomorfe si possono costruire soluzioni dell'equazione di Laplace in dominii diversi.