Section outline

  • Collapse Expand

    Annunci

    Collapse all Expand all




    • Annunci Forum
      Sono state aggiornate le note del corso. 
  • Collapse Expand

    Note aggiornate 2024-2025

    • Riassunto dei cambiamenti File

      Elenco dei cambiamenti rispetto alle note del 2023-2024. Si veda anche la pagina campusnet per un riassunto dettagliato degli argomenti che abbiamo trattato. 

    • Complementi di analisi complessa (lezioni 1-2) File

      Questa parte delle note e` quasi identica a quelle del 2022-2023. E` stato aggiunto il calcolo di un integrale calcolato sul cammino "Pac-Man", discusso a lezione. 

    • Special_Functions (lezioni 3-4-5) File

      Rispetto alle note del 2023-2024, e` stata aggiunta una parte piu` dettagliata sul metodo di Laplace (o metodo del punto a sella). Sono state trattate solo le funzioni Gamma, Zeta e Ipergeometriche generalizzate, mentre non sono state trattate le funzioni Poligamma e i Polilogaritmi. 

    • Equazioni Differenziali Ordinarie parte 1 - (lezioni 6-7-8) File

      E` stata aggiunta alle note una parte sui problemi di bordo per equazioni lineari, ed espansa la parte sulle funzioni di Green (il contenuto della lezione 8). 

    • Equazioni Differenziali Ordinarie parte 2 - lezioni 9 -10 - 11 - 12- Espansioni in serie e metodi perturbativi File

      NOTA: Rispetto alle note dello scorso anno, non e` piu` presente la parte sul metodo di Papperitz-Riemann. 

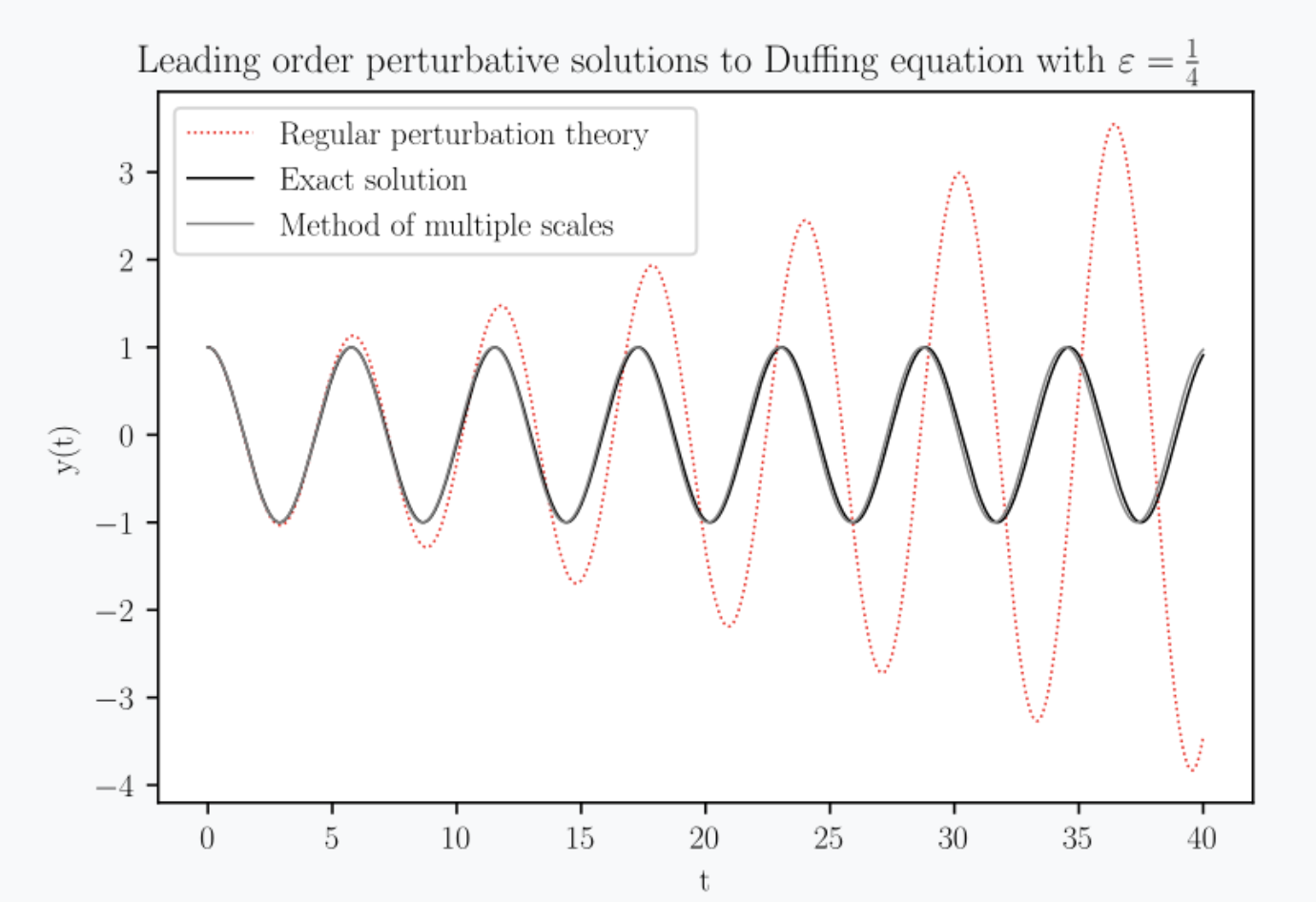
      NEW: Sono presenti due parti nuove (lezioni 10-11) su metodi perturbativi in casi singolari: il metodo dei boundary layers e il metodo delle scale multiple. Questi metodi non saranno oggetto di esercizi ma faranno parte degli argomenti possibili di discussione all'orale. Si noti anche il metodo di espansione intorno a punti irregolari singolari, che puo` essere argomento di esercizi per l'esame scritto.  

    • Note PDE I: Metodo Caratteristiche - lezioni 13-14-15-16 File

      Questa parte delle note e` la stessa rispetto a quelle del 2023-2024. Nota: l'argomento principale della lezione 15, cioe` la trattazione degli shock e delle soluzioni deboli dell'equazione di Burgers e` contenuta in una parte successiva delle note. 

    • Note_Eq_Onde_1 - lezione 17 File

      NEW: E` stata aggiunta la discussione delle funzioni di Green, trattata nella lezione 17. 

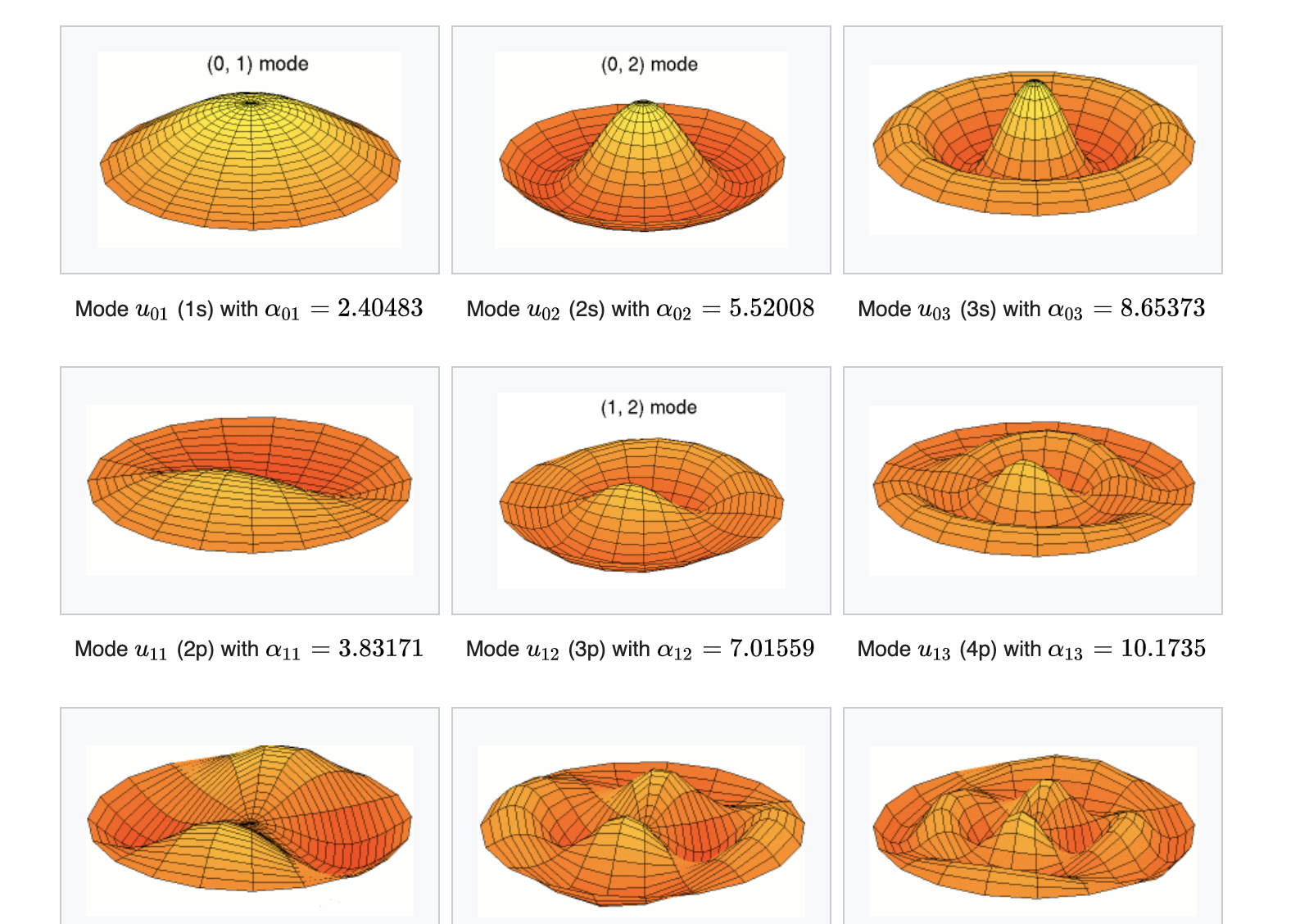
    • Note_Eq_Onde_2_Problemi_di_Bordo_e_Autofunzioni_In_Higher_D_(lezioni 18-19-22) File

      Questa parte delle note e`  identica a quella del 2023-2024. Le note includono anche la trattazione delle soluzioni dell'equazione di Helmholtz in dominio sferico, che NON sono state trattate quest' anno. Abbiamo trattato solo il caso del dominio cilindrico, con l'esempio dello studio delle oscillazioni di una membrana circolare. 

    • Heat_Equation (lezioni 20 e 22) File

      Rispetto alle note dello scorso anno, ci sono piccoli cambiamenti: e` stata aggiornata la parte delle note sulla relazione tra soluzione fondamentale (heat kernel) e funzione di Green, e sono state fatte piccole correzioni di sviste in alcune formule nella parte sulla separazione delle variabili. 

      Si noti che l'ultima parte del documento sui problemi matematicamente ben posti o mal posti NON e` stata discussa a lezione e non e` parte del programma. 

    • Note_Burgers_Equation_part_II (lezioni 15 e 21 ) File

      Questa parte delle note e` identica a quelle del 2023-2024.

    • Note_Laplace-Poisson_(lezioni 23-24) File

      Questa parte delle note e` identica al 2023-2024. NOTA: il metodo delle immagini e` stato trattato solo nel caso del semi-piano, non nel caso del disco. Nel caso del disco e` importante pero` saper risolvere il problema con il metodo delle autofunzioni. 

  • Collapse Expand

    Note utili di corsi in altre universita`

  • Collapse Expand

    Esempi di prove d'esame passate

  • Collapse Expand

    Note anno scorso 2023-2024

  • Collapse Expand

    Esercizi

  • Collapse Expand

    Risorse per approfondimenti

    • Digital Library of Mathematical Functions URL
    • Why are special functions special? File
      Articolo del famoso fisico matematico Michael Berry
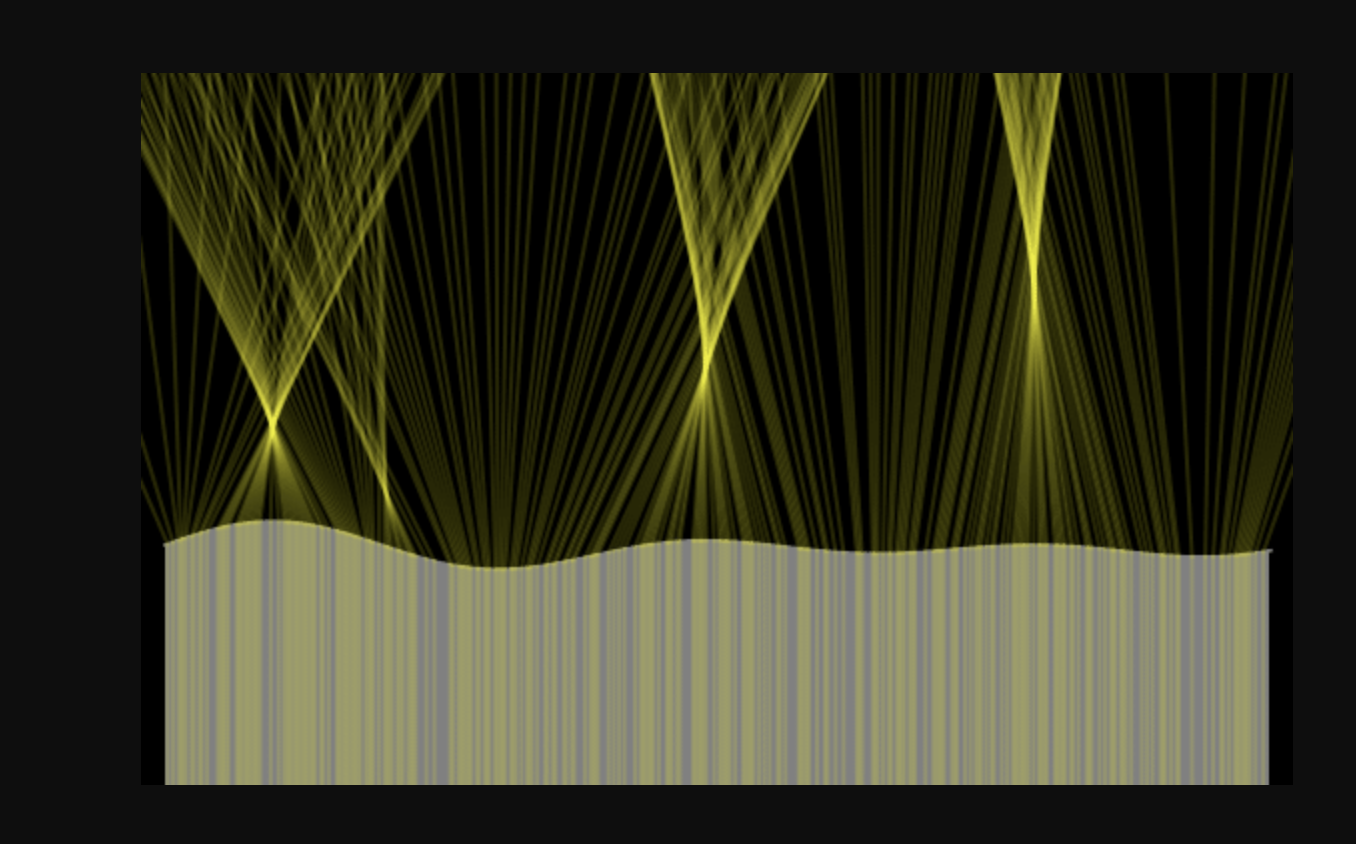
    • Teoria dell'arcobaleno di Airy (in cui la funzione di Airy vista a lezione descrive le frange sovranumerarie) URL

      Spiegazione della derivazione della funzione oscillante di Airy per il profilo intensita` della luce dell'arcobaleno in funzione dell'angolo rispetto all'orizzonte. Spiega la comparsa delle frange sovranumerarie sotto l'arcobaleno principale.

    • programma di calcolo simbolico per risolvere equazione di Burgers File

      Con un qualsiasi programma di calcolo simbolico (Maple, Mathematica, Python (open access), o molti altri), si puo` facilmente adattare il programma per generare una soluzione dell'equazione di Burgers con profilo iniziale a piacere. Il metodo si puo` generalizzare per risolvere nello stesso modo, con il metodo delle curve caratteristiche, qualsiasi PDE con derivate del prim'ordine. 

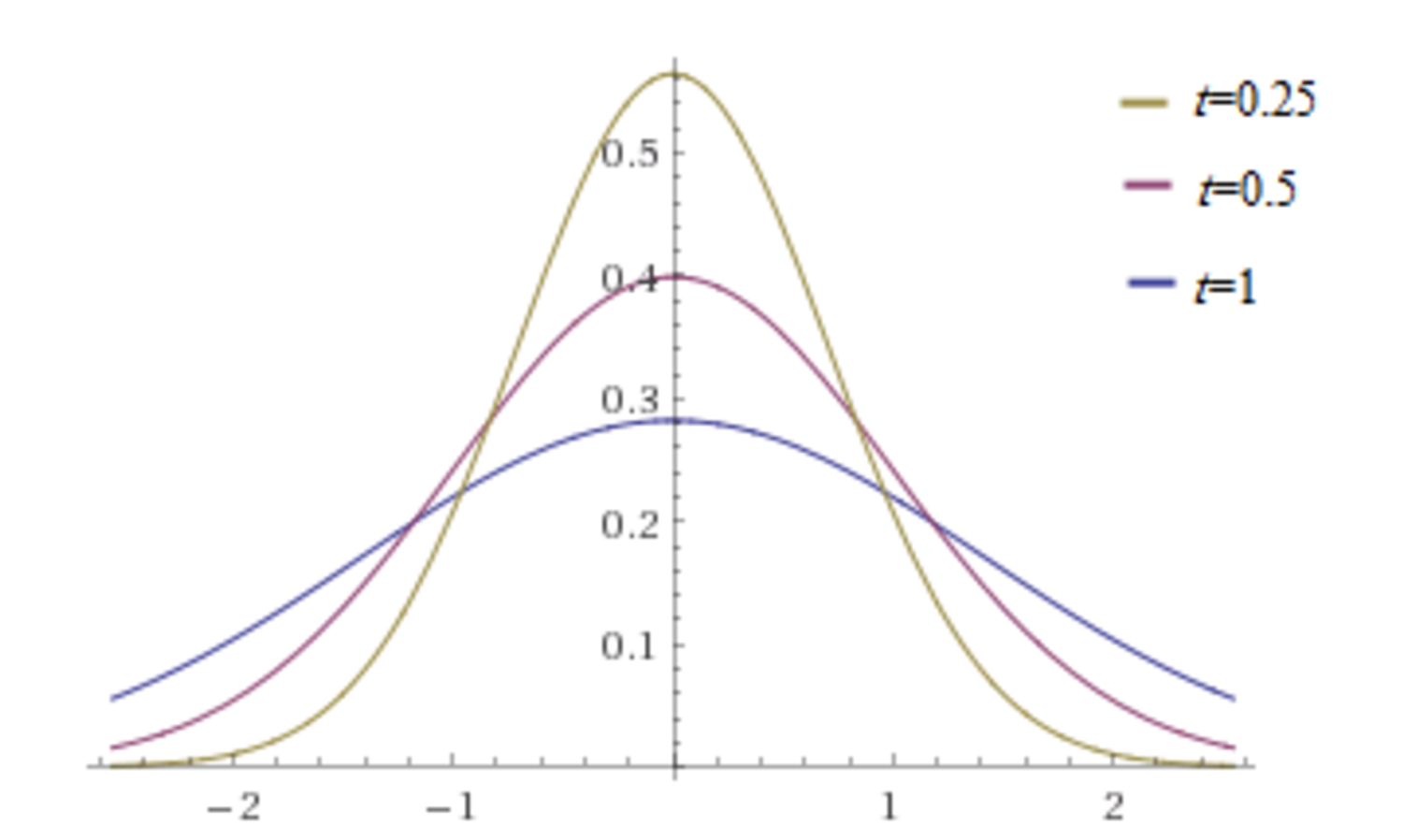
    • simulatore online equazione delle onde 1D URL
    • Simulatore online equazione calore URL

      Simulatore online equazione calore. Sperimentando con i dati iniziali si puo` notare come anche dati iniziali  irregolari, diventano istantaneamente differenziabili. Notare gli effetti diversi delle condizioni di contorno di Dirichlet e Neumann sulla soluzione di equilibrio raggiunta a tempi grandi. 

    • Video su comportamento equazione KdV e solitoni (discussi nella lezione 20). URL

      Video sull'evoluzione equazione KdV con profilo iniziale cos(x) e condizioni di bordo periodiche. Si noti come nei primi istanti la soluzione evolve in modo simile all'equazione di Burgers inviscida, fino quasi a formare un fronte di shock. La soluzione pero` rimane a un sol valore, e si decompone in una sequenza di solitoni, che dominano la dinamica successiva. I solitoni interagiscono elasticamente e il loro numero non cambia. 

    • Can you hear the shape of a drum? URL
      Presentazione su equazione delle onde e musica all'universita` di Oxford.
    • Notes on Physics of Music File

      Note da un corso universitario dell'universita` di McGill per chi volesse approfondire la fisica degli strumenti musicali.

    • Per chi volesse approfondire il legame tra funzione Zeta di Riemann e numeri primi:

      Libro di Edwards "The Riemann Zeta function", in particolare sez. 1.11 e sezione 3. In appendice contiene anche una traduzione dell'articolo originale di Riemann. http://www.stat.ucla.edu/~ywu/Riemann.pdf

      Un riassunto moderno dell'articolo di Riemann si trova qui: https://arxiv.org/pdf/1609.02301.


  • Collapse Expand

    Lezione 1 - Cosa puo` succedere nel piano complesso?


    • Illustrazione della superficie di Riemann della funzione radice quadrata di z. 

    • notebook Mathematica dimostrazione tagli di funzioni analitiche File
    • Illustrazione fogli di alcune funzioni polidrome File

    • Argomenti trattati:

      Introduzione: l'uso della continuazione analitica da parametri reali a complessi in alcuni problemi di fisica. 

      Principio della continuazione analitica. Alcuni teoremi sulla continuazione analitica, teorema di Liouville e altri risultati che dimostrano la rigidita` delle funzioni olomorfe. 

      Tipi di possibili singolarita` delle funzioni olomorfe, in particolare discussione dei punti di diramazione. 

      Concetto di punto di diramazione, taglio, foglio di Riemann e superficie di Riemann.

      Esempio della funzione radice quadrata e altre funzioni semplici. 

  • Collapse Expand

    Lezione 2. Esempio di integrali calcolati grazie i tagli, e relazioni di dispersione di Kramers-Kronig.


    • Argomenti trattati:

      Concetto di ordine di un punto di diramazione.

      Discussione di alcune funzioni olomorfe con due punti di diramazione al finito, in cui il punto all'infinito puo` essere o meno un punto di diramazione. 

      Uso delle proprieta` delle funzioni polidrome per il calcolo dell' integrale di x^a/(1+x^2), con -1<a<1 (cammino "Pac-Man").

      Derivazione delle relazioni di Kramers-Kronig, applicazione fisica alla relazione tra dispersione e dissipazione del campo elettrico in un mezzo dielettrico nell'approssimazione lineare.  Relazione tra principi fisici (causalita`, linearita`, invarianza temporale) e proprieta` analitiche.

  • Collapse Expand

    Lezione 3: introduzione alle funzioni speciali e funzione Gamma


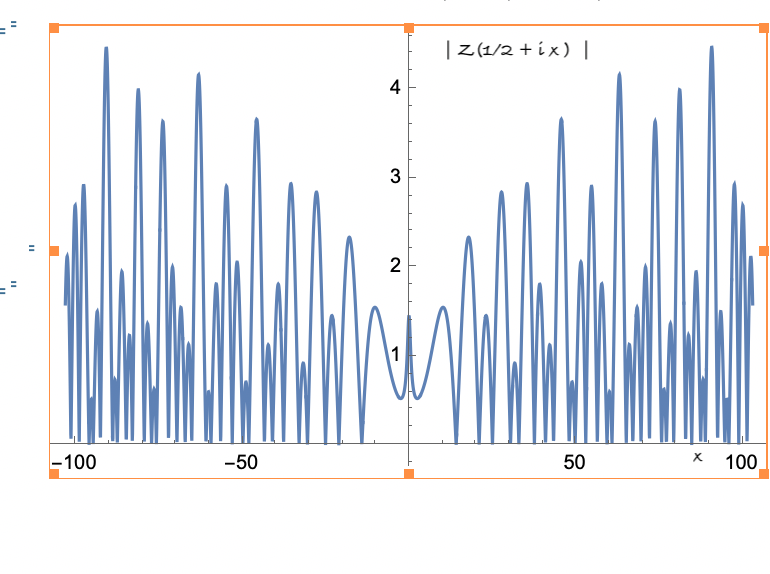
    Il grafico mostra il valore assoluto della funzione Gamma di Eulero nel piano complesso.

    • Argomenti discussi:

      Introduzione alle funzioni speciali. 
      Funzione Gamma di Eulero: rappresentazione integrale e regione di validita` ; relazione di ricorrenza ; posizione dei poli della funzione Gamma ; relazione con il fattoriale dei numeri interi ; relazione di riflessione. 
      Il metodo di Laplace (discussione euristica) e il suo utilizzo per calcolare l'approssimazione di Stirling del fattoriale. 
      Il concetto di serie asintotica e le differenze dalle serie convergenti ordinarie (con l'esempio della serie di Stirling). 


  • Collapse Expand

    Lezione 4: Zeta di Riemann

    • Valore assoluto della funzione Zeta di Riemann sulla linea critica.


    • Nella figura sono illustrate le proprieta` principali della Zeta di Riemann.


    • La funzione che conta i numeri primi. Attraverso il legame tra numeri primi e Zeta di Riemann si riesce a stabilire il comportamento per grande argomento della funzione (quindi informazione sulla distribuzione asintotica dei numeri primi). 

    • Fine discussione formula di Stirling, sue correzioni e proprieta` delle serie asintotiche. Abbiamo enfatizzato come funzioni diverse possano avere la stessa serie asintotica, e il fatto che  termini esponenzialmente piccoli siano invisibili rispetto a serie asintotiche di potenze.

      Inizio studio Zeta di Riemann; definizione come serie e come integrale, dominio di convergenza. 

      Relazione con funzione Eta di Dirichlet che permette di estendere Zeta alla striscia critica.

      Formula di riflessione che permette di estendere la Zeta a tutto il piano complesso. 

      Proprieta` analitiche, posizione del polo e degli zeri "banali" dalla formula di riflessione. 

      Ipotesi di Riemann sulla posizione degli infiniti zeri non banali.  


  • Collapse Expand

    Lezione 5: fine Zeta di Riemann e funzioni ipergeometriche

    • Argomenti trattati:

      Abbiamo discusso la formula di Eulero che lega la Zeta di Riemann ai numeri primi. 

      Abbiamo discusso senza dimostrazione alcuni risultati che legano alcune funzioni discrete che "contano" i numeri primi con la distribuzione degli zeri della Zeta di Riemann (si veda la sezione approfondimenti per chi volesse esplorare ulteriormente questo argomento). 

      Funzioni ipergeometriche: loro definizione come serie, convergenza della serie. Funzioni ipergeometriche di Gauss, loro rappresentazione integrale e equazione differenziale che soddisfano: abbiamo notato come sia un'equazione differenziale con esattamente tre punti singolari, tutti fuchsiani. 

      Breve introduzione alle equazioni differenziali ordinarie. 


    • Grafico che illustra la funzione ipergeometrica di Gauss 2F1 per una certa scelta di parametri. E` visibile il punto di diramazione in  z = 1 (con un taglio che lo connette a infinito per z>1). La funzione per questa scelta di parametri diverge nel punto di diramazione. Il punto z=0 e` regolare. 

  • Collapse Expand

    Lezione 6: Equazioni differenziali ordinarie: metodi diretti.

    • Inizio discussione equazioni differenziali ordinarie. 

      Richiami sul teorema di esistenza e unicita`. Abbiamo visto un controesempio [y' = Yes^(1/3) ] in cui sono violate le condizioni del teorema nel punto y(0) = 0, e l'equazione ammette piu` soluzioni del problema a valori iniziali.

      Esempio di problema a valori di bordo  [y''(x) + lambda y(x) = 0 con y(0) = y(L) = 0]. Abbiamo visto come l'esistenza o meno di soluzioni non nulle dipenda da lambda: si hanno soluzioni non nulle solo per lambda = ((n Pi)/L )^2 per n intero positivo. 

      Abbiamo visto alcuni metodi diretti per la soluzione di equazioni differenziali semplici: le equazioni separabili, le equazioni in forma di differenziale esatto (metodo del potenziale), e equazioni lineari a coefficienti costanti. 

      Abbiamo iniziato a parlare di equazioni lineari a coefficienti non costanti introducendo il Wronskiano. 


    • Forma della funzione potenziale nell'esempio risolto a lezione (anche sulle note) sul metodo del differenziale esatto. 

      Forma di una particolare soluzione dell'equazione differenziale ottenuta come superficie di livello del potenziale. Si noti che la funzione y(x) ha due rami distinti. Il punto in cui y'(x) = infinito e` un punto in cui non si applicano le condizioni del teorema di esistenza e unicita`. 

  • Collapse Expand

    Lezione 7: equazioni differenziali lineari omogenee e inomogenee

    • Argomenti trattati:

      Abbiamo visto un esempio di calcolo esplicito di Wronskiano per un'equazione lineare. Abbiamo notato come il Wronskiano si annulli in un punto. Un problema alle condizioni iniziali in quel punto non e` ben definito. 

      Abbiamo discusso  il metodo di variazione delle costanti per generare nuove soluzioni di un'equazione lineare a partire da soluzioni note.

      Abbiamo poi discusso equazioni inomogenee. Abbiamo visto il metodo della funzione di Green per costruire soluzioni particolari dell'equazione inomogenea a partire da una base completa di soluzioni del problema omogeneo. 

      Abbiamo trattato il caso del calcolo della funzione di Green in un problema di equazione differenziale di ordine 1. 

  • Collapse Expand

    Lezione 8 - Metodo della funzione di Green e problemi di bordo.

    • (LE NOTE SU QUESTA PARTE SONO STATE AGGIORNATE).

      Abbiamo calcolato la funzione di Green per un problema ai valori iniziali per un'equazione del second ordine.

      Abbiamo discusso proprieta` generali dei problemi con condizioni di bordo regolari, in particolare il seguente "teorema dell'alternativa":  un problema alle condizioni di bordo omogeneo ha solo la soluzione banale, se e solo se ogni problema problema inomogeneo associato ammette una e una sola soluzione. 

      Abbiamo osservato come le condizioni del teorema sono equivalenti al fatto che la matrice costruita con le condizioni di bordo valutate su una base di soluzioni abbia determinante non nullo.

      Abbiamo illustrato il calcolo della funzione di Green per due problemi di bordo, uno definito su un intervallo e uno (un caso limite) sulla retta reale. 

      (Le note su questa parte verranno aggiornate al piu` presto).

  • Collapse Expand

    Lezione 9 - Metodi di espansione in serie nella variabile.

    • Abbiamo descritto metodi di risoluzione o analisi di un'equazione differenziale ordinaria lineare di ordine 2 tramite espansione in serie nella variabile. 

      Abbiamo distinto punti regolari, singolarita` fuchsiane e singolarita` irregolari, spiegando come costruire una base di due soluzioni intorno  a un punto regolare, o una singolarita` fuchsiana, tramite una serie convergente. 

      Per le singolarita` fuchsiane in particolare abbiamo riepilogato come ottenere l'equazione indiciale. 

      Abbiamo visto esplicitamente l'esempio della soluzione per serie dell'equazione di Airy, che ci ha permesso di scrivere la soluzione come sovrapposizione di due funzioni ipergeometriche calcolando esplicitamente i coefficienti delle serie. 

      Abbiamo riepilogato come classificare il comportamento del punto all'infinito, e notato che si tratta di una singolarita` irregolare per l'equazione di Airy. Nella prossima lezione capiremo come ottenere il comportamento asintotico in questo punto. 


    • Grafico delle due funzioni di Airy, soluzioni indipendenti dell'equazione y''(x) = x y(x). 

  • Collapse Expand

    Lezione 10 - Sviluppo intorno a punti irregolari: il metodo dell'equilibrio dominante

    • Abbiamo discusso il metodo dell'equilibrio dominante per comprendere il comportamento delle soluzioni di un'equazione differenziale (lineare omogenea, negli esempi visti) intorno a una singolarita` irregolare. 

      Come primo esempio abbiamo visto come dedurre i due possibili comportamenti delle soluzioni dell'equazione di Airy y''(x) = x y(x) per x->+ infinito. 

      Nel caso dell'equazione di Airy, l'equilibrio dominante a infinito e` dato da (S')^2 ~ x , con |S''|<< (S')^2, dove S(x) = Log[ y(x) ]. Abbiamo visto come verificare che altre possibili ipotesi per l'equilibrio dominante portano (in questa equazione, in questo limite) a delle inconsistenze.

      Abbiamo visto cosa cambia espandendo invece per x -> - infinito. 

      Abbiamo visto come calcolare successivi ordini sottodominanti dell'espansione di S(x) = Log[y(x) ], iterando il metodo. Abbiamo discusso come sia necessario calcolare l'espansione di S(x) fino a quando non si trovino termini asintoticamente piccoli, per poter fissare il "fattore di controllo" del comportamento asintotico di y(x). Ad esempio, nel caso dell'equazione di Airy a x_>+oo, e` necessario calcolare S(x) ~ +- 2/3 x^(3/2) -1/4 Log[x] + O(x^(-3/2) ), in modo da poter concludere che y(x) ~ exp( +- 2/3 x^(3/2) )/x^(1/4) .

      Abbiamo notato come, per espansione intorno a punti fuchsiani (o punti che siano legati a punti fuchsiani da un cambio di variabile), si abbia, come ordine di grandezza, un tipico equilibrio dominante, della forma (S')^2 ~ S'', che implica un andamento logaritmico per S(x) nel punto in questione. 

      Abbiamo poi discusso un esempio di equazione che presenta due equilibri dominanti ancora diversi. Questo secondo esempio e` costituito dall'equazione x^2 y''(x) + (1+ 3 x) y'(x) +y(x) = 0, di cui abbiamo studiato l'espansione  per x->0^+.  In questo caso, ci sono due scelte indipendenti, entrambe consistenti, di equilibrio dominante. Definendo S(x) = Log[y(x)], nel primo caso S' ~ 1 , che porta a una soluzione data da una serie in potenze di x, y(x) ~ 1 - x + ....  (serie asintotica, non convergente). Nel secondo caso x^2 (S')^2 ~-S' , che porta a una soluzione con andamento y(x) = exp[ 1/x ]/x (1 + ....)

  • Collapse Expand

    Lezione 11 - Introduzione ai metodi perturbativi. Perturbazioni regolari vs boundary layers

    • (LE NOTE SU QUESTA PARTE SONO STATE AGGIORNATE- SI VEDA SEZIONE INIZIALE SU MOODLE).

      Abbiamo iniziato a discutere metodi perturbativi per equazioni differenziali che contengano un parametro piccolo (che chiameremo epsilon).

      Abbiamo visto un esempio di costruzione di serie perturbativa per risolvere l'equazione y''(x) = epsilon f[x] y(x) con una condizione iniziale in x = 0. Abbiamo considerato esplicitamente il caso f[x] = x.   (cosi` che per epsilon = 1 si ritrova l'eq. di Airy) ,  ma il metodo funziona per qualunque f[x] continua su un certo intervallo finito. 

      Questo e` un esempio di espansione perturbativa regolare se guardiamo la soluzione su un intervallo finito. La serie in potenze epsilon converge piu` rapidamente (nel caso di Airy, due volte piu` rapidamente) di un'espansione perturbativa della stessa equazione costruita espandendo nella variabile x. 

      Abbiamo poi discusso come in molti problemi si trovino invece esempi di teoria delle perturbazioni singolare. Il caso tipico e` quando il parametro di espansione moltiplica il termine con la derivata piu` ampia. 

      Abbiamo discusso come in molti esempi di perturbazioni singolari, il comportamento per epsilon = 0 sia qualitativamente diverso da quello per epsilon diverso da zero, per quanto epsilon sia piccolo. Tipicamente, per epsilon piccolo ma non nullo, si formano regioni di rapida variazione della soluzione, in cui la soluzione perturbativa costruita nel modo standard non si applica. 

      Un tipico esempio di questo fenomeno e` quello dei "boundary layers" (anche noti come "strati limite"): regioni di rapida variazione della soluzione, la cui larghezza tende a zero per epsilon tendente a zero. Abbiamo considerato l'esempio dell'equazione

      epsilon y''(x) + (1 + epsilon) y'(x) + y(x) = 0 ,      con condizioni di bordo y(0) = 0 e y(1) = 1 ,

      per studiare come trattare problemi con boundary layers. In questo caso, si forma un boundary layer la cui larghezza scala come epsilon intorno  al punto x = 0. 

      Abbiamo costruito due termini di un'espanzione perturbativa "esterna" valida per x finito e epsilon piccolo, e due termini di un'espansione perturbativa alternativa, "interna", che vale per x = epsilon X , con X finito, cioe` "dentro" al boundary layer. 

      Abbiamo poi visto come bisogni considerare una regione intermedia tra i due regimi precedenti per "incollare" le due espansioni perturbative interna e esterna, fissando i parametri liberi.

      Come riprenderemo durante la prossima lezione, questa tecnica di incollare le due espansioni interna ed esterna permette di costruire un'approssimazione globale, valida uniformemente per qualunque x per epsilon piccolo. 


  • Collapse Expand

    Lezione 12 - Fine boundary layers. Metodo delle scale multiple.

    • LE NOTE SU QUESTA PARTE SONO STATE AGGIORNATE- SI VEDA SEZIONE INIZIALE SU MOODLE


      Nella figura: confronto tra teoria perturbativa standard, che da un risultato completamente errato, e approssimazione del prim'ordine ottenuta con il metodo delle scale multiple, per l'equazione di Duffing. 

      in questa lezione abbiamo finito di descrivere il metodo dei boundary layers, sullo stesso esempio della scorsa lezione e anche considerando un'equazione leggermente piu` complessa , epsilon y''(x) + (1+x ) y'(x) + y(x) = 0, con y(0) = y(1) = 1, per la quale abbiamo calcolato l'approsimazione del prim'ordine con il metodo delle due espansioni asintotiche (interna e esterna al boundary layer) incollate.

      In seguito, abbiamo descritto il metodo delle scale multiple, sull'esempio dell'equazione di Duffing y''(t) + y(t) + epsilon y^3(t) = 0, con condizioni iniziali y(0) = 1, y'(0) = 0. Abbiamo mostrato come il metodo delle scale multiple possa essere usato per rimuovere i termini "secolari", e portare all'approssimazione del prim'ordine y(t) = cos(t + 3/8 epsilon t ). 

    • Registrazione parte 1 URL
    • registrazione parte 2 URL
    • Esempi di confronto tra approssimazione boundary layers e soluzioni esatte. File
  • Collapse Expand

    Lezione 13 - Equazioni a derivate parziali. Soluzione generale per equazioni lineari di ordine 1.

    • Abbiamo iniziato a discutere di equazioni alle derivate parziali (PDE). Abbiamo discusso il concetto di equazioni lineari, quasi-lineari e completamente nonlineari, e discusso di come in alcuni casi il problema di Cauchy alle condizioni iniziali puo` non avere soluzione nel caso delle equazioni a derivate parziali. 

      Abbiamo visto come risolvere in modo generale equazioni di ordine 1 con il metodo delle caratteristiche, discutendo alcuni esempi. 

      Abbiamo poi trattato in dettaglio l'esempio dell'equazione del trasporto lineare, discutendo anche di come risolverla in presenza di un termine inomogeneo. 

      Alla fine della lezione abbiamo iniziato a discutere di come usare il metodo delle curve caratteristiche per equazioni quasi-lineari, dimostrando che le curve caratteristiche (definite come curve integrali di equazioni differenziali ordinarie costruite con i coefficienti dell'equazione) sono curve che giacciono sempre sul grafico delle soluzioni della PDE.

    • Registrazione lezione 13 URL
  • Collapse Expand

    Lezione 14 - Curve caratteristiche e shock per equazioni quasi-lineari.

    • Abbiamo studiato il metodo delle curve caratteristiche per equazioni quasi -lineari con alcuni esempi, in particolare considerando problemi con condizioni iniziali date su una curva (problema di Cauchy).

      Abbiamo visto come, anche se la soluzione e` solo data in forma implicita (non sempre e` possibile invertire la parametrizzazione data dalle curve caratteristiche), si puo` sempre usarla per generare un grafico delle soluzioni. Per alcuni esempi di grafici generati in questo modo in Mathematica si veda il file pdf allegato. 

      Abbiamo discusso le condizioni che garantiscono l'esistenza e unicita` locale delle soluzioni del problema di Cauchy (problema delle condizioni iniziali su una curva). Abbiamo visto un esempio in cui le condizioni del teorema sono violate e infatti la soluzione diventa a due valori in un intorno della curva di Cauchy.

      Abbiamo poi discusso l'equazione di Burgers inviscida (o equazione del trasporto nonlineare), che e` un prototipo dell'importante fenomeno di formazione degli shock dovuto alla nonlinearita`.

      Abbiamo brevemente discusso il ruolo di questa equazione come analogo delle equazioni di Eulero nel caso di una dimensione spaziale (e una temporale). 

      Abbiamo poi discusso la soluzione dell'equazione di Burgers con profilo iniziale arbitrario, mostrando come in molti casi l'evoluzione temporale porta alla formazione di una singolarita` in cui il gradiente della soluzione u_x diverge. Abbiamo discusso come calcolare il tempo in cui avviene questa singolarita`, e come dopo questo istante la soluzione diventi a piu` valori.

    • Registrazione di parte della lezione URL

      Purtroppo per un problema tecnico e` stata registrata solo la prima parte della lezione 14. Gli argomenti trattati seguono comunque le note e sono reperibili registrazioni su questi argomenti su Moodle degli scorsi anni.

    • Illustrazioni di soluzioni, grafici mostrati a lezione. File

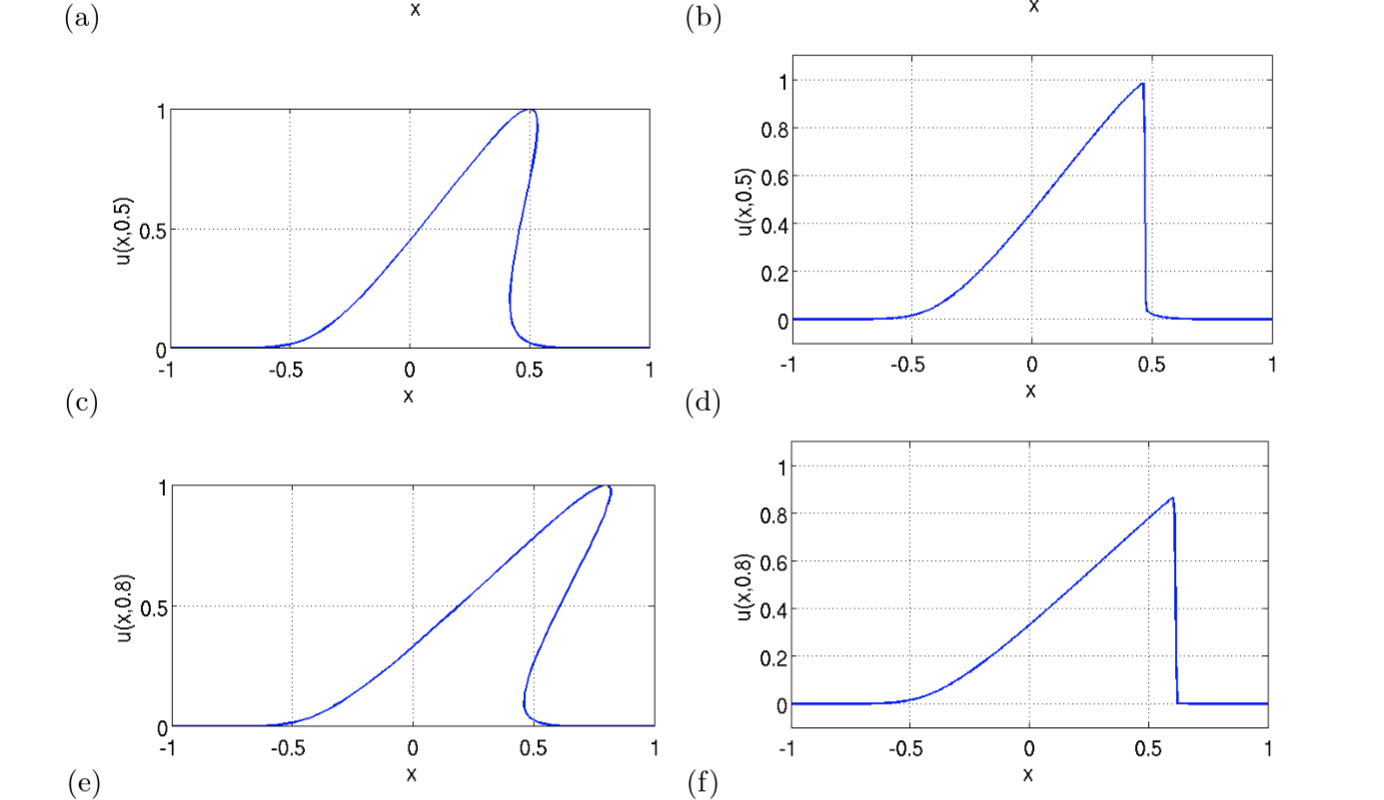
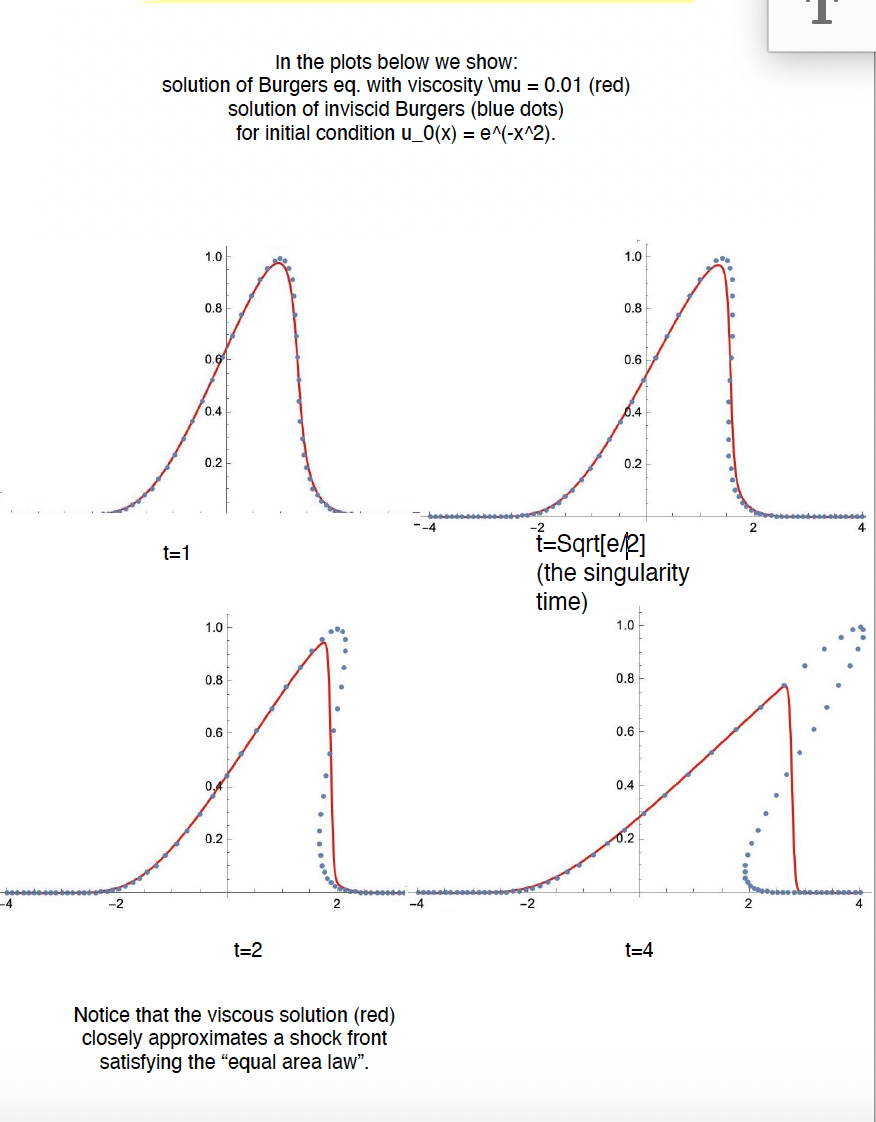
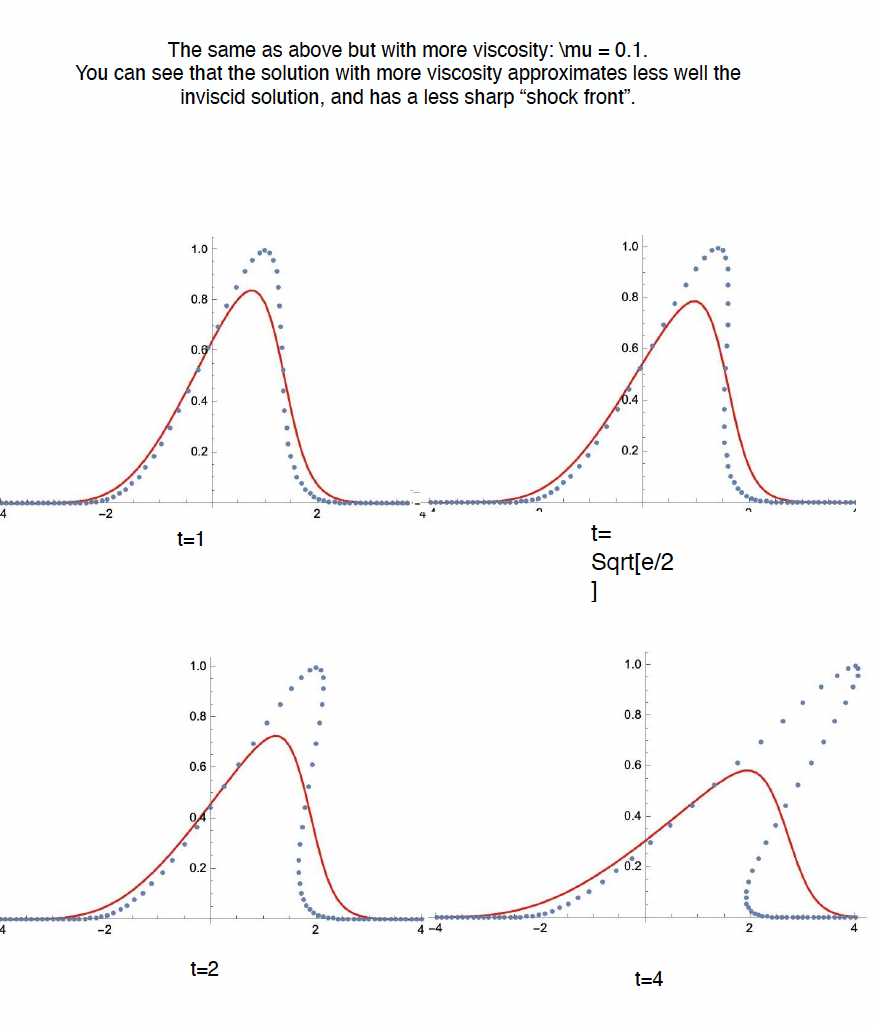
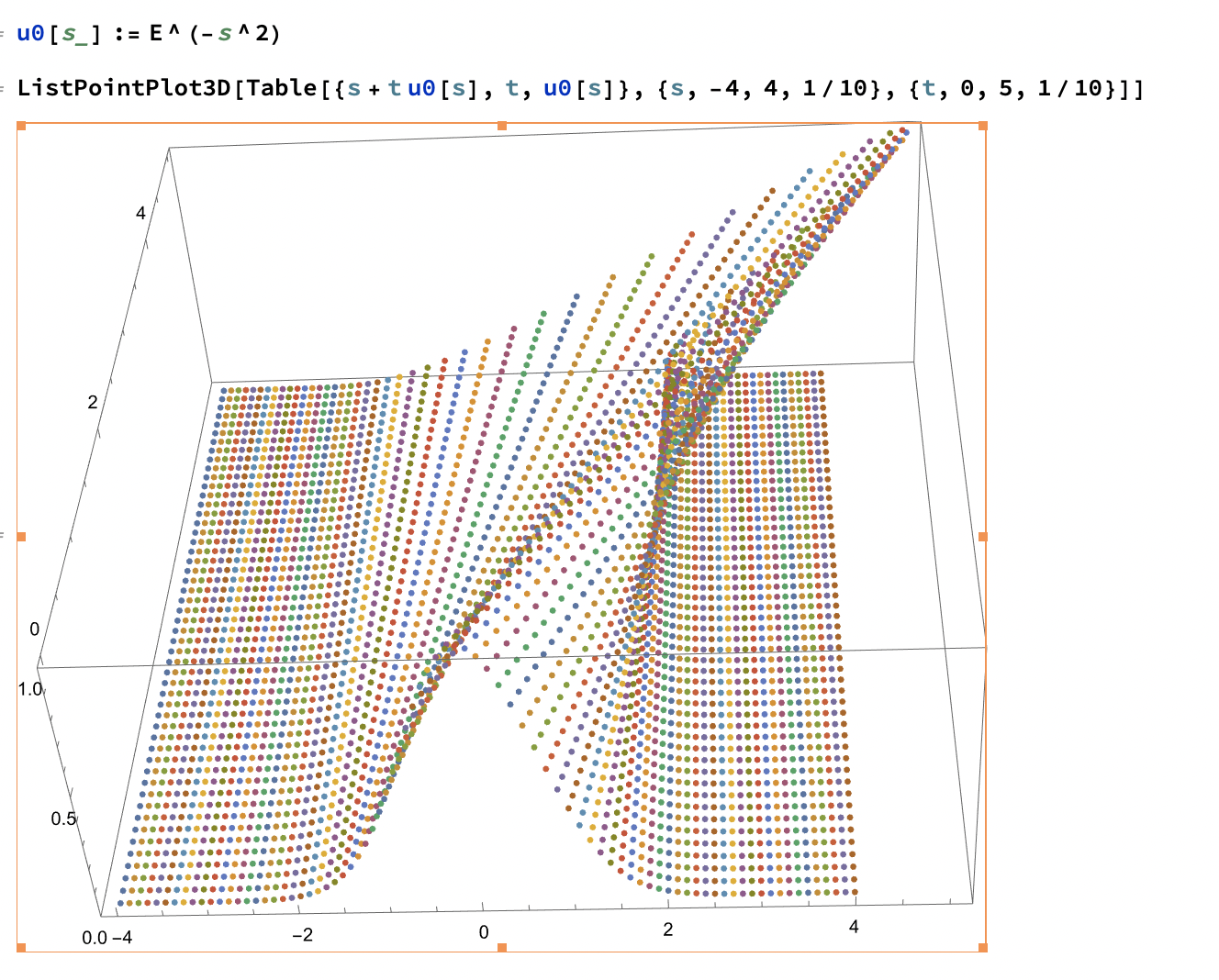    • Fenomeno di formazione di una singolarita` per una soluzione dell'equazione di Burgers inviscida, con profilo iniziale gaussiano, risolta con il metodo delle caratteristiche. I semplici comandi in Mathematica illustrano come realizzare il grafico della soluzione a tempi generici. Sopo la formazione della singolarita` la soluzione diventa a piu` valori. 

  • Collapse Expand

    Lezione 15. Soluzioni deboli con shock. Equazioni completamente nonlineari.

    • Abbiamo discusso come costruire soluzioni a un sol valore (ma discontinue), dopo il tempo di formazione di uno shock nell'equazione di Burgers, "tagliando" la soluzione a piu` valori lungo un fronte di shock discontinuo. 

      Abbiamo discusso il concetto di soluzione in senso debole di una legge di conservazione, e ricavato la condizione di Rankine-Hugoniot per la velocita` del fronte di shock.

      Abbiamo poi discusso il metodo per risolvere equazioni completamente nonlineari di ordine 1, trattando un esempio nel caso dell'equazione eikonale. 

    • cartella con registrazioni URL


    • Soluzioni a piu` valori costruite con il metodo delle caratteristiche, e le corrispondenti soluzioni deboli con shock discontinui. 

  • Collapse Expand

    Lezione 16: applicazioni dell'equazione eikonale. Esempi di soluzione problemi con metodo caratteristiche. .

    • Abbiamo discusso due interpretazioni fisiche dell'equazione eikonale: come equazione che descrive la forma dei fronti d'onda per la propagazione di onde in un mezzo nell'approssimazione eikonale (appunto) che porta all'interpretazione dell'ottica geometrica. I fronti d'onda sono le superfici di livello della soluzione dell'equazione eikonale, e le traiettorie dei raggi di luce sono le stesse delle curve caratteristiche di questa equazione.

      La seconda interpretazione descrive la forma delle dune di sabbia.

      Abbiamo commentato sul significato delle singolarita` dell'equazione, che sono punti in cui le caratteristiche si ripiegano su se stesse. In una interpretazione questa singolarita` diventano le caustiche formate dai raggi di luce, nel caso delle dune di sabbia le stesse singolarita` si possono osservare come "creste".

      Abbiamo svolto due esempi di analisi di problemi (uno quasilineare, uno completamente nonlineare) con il metodo delle caratteristiche. In entrambi i casi abbiamo ricavato la soluzione in forma implicita, e nel primo caso abbiamo studiato il tempo di formazione di una singolarita` (di tipo shock). 

      Abbiamo poi iniziato a parlare di equazioni di ordine 2, discutendo la classificazione delle equazioni  in due variabili con termine di second'ordine lineare in equazioni iperboliche (tipo eq. delle onde), paraboliche (tipo eq. del calore) e ellittiche (tipo eq. di Laplace). 

    • link a cartella con la registrazione URL


  • Collapse Expand

    Lezione 17 - Onde in spazio infinito

    • -- Purtroppo per un problema tecnico non e` stata salvata la registrazione di questa lezione --

      [E` STATA AGGIORNMATA SULLE NOTE LA PARTE SULLE FUNZIONI DI GREEN ]

      In questa lezione abbiamo studiato problemi ai valori iniziali per l'equazione delle onde, anche con un termine forzante inomogeneo, per propagazione in spazio infinito, senza bordi.

      Caso unidimensionale. Problema di Cauchy e soluzione (formula di d'Alembert). 

      Poi abbiamo considerato il metodo della funzione di Green per l'equazione delle onde in dimensione generica, per costruire una soluzione dell'equazione inomogenea. Facendo una trasformata di Fourier sulle variabili spaziali, ci siamo ridotti al problema di calcolare la funzione di Green per un'equazione differenziale ordinaria nella variabile temporale. 

      Abbiamo trovato la formula generale (valida in qualsiasi dimensione) per la trasformata di Fourier spaziale della funzione di Green. 

      Abbiamo discusso come questa forma si trasformi in espressioni con proprieta` diverse se si fa l'antitrasformata: in particolare, per D dispari >=3 la funzione di Green e` localizzata su fronti d'onda sferici che viaggiano con velocita` c .

      Abbiamo commentato il caso D = 3. Abbiamo scritto la formula per la soluzione del problema inomogeneo con condizione iniziale nulla a tempo generico, che si riduce alla soluzione con il potenziale ritardato tipica dell'elettromagnetismo se si impone condizione iniziale nulla a tempo -oo. 

      Abbiamo poi discusso la forma della soluzione del problema di Cauchy per l'equazione delle onde omogenea in D = 3, con dati iniziali generici. 

      Abbiamo finito commentando le differenze tra questo caso e il caso D=2, Mentre in D=3 la funzione di Green e` localizzata  sui fronti d'onda sferici, nel caso 2D la f. di Green ha supporto anche all'interno delle superfici sferiche che racchiudono. 

      Questo sottende un fenomeno particolare, per cui in un mondo D=2 i suoni avrebbero avrebbero durata infinita (per quanto sarebbero via via attenuati). Il rumore prolungato del tuono e` dovuto alla propagazione quasi-2D delle onde sonore che si generano intorno al fulmine. 

    • Note su funzioni di Green, da un corso di Univ. Cambridge URL
  • Collapse Expand

    Lezione 18 - Problemi con bordi e metodo di Fourier

    • Abbiamo discusso come trattare problemi con condizioni di bordo omogenee per l'equazione delle onde.

      Prima abbiamo considerato il caso del problema su una linea semi-infinita, che si puo` trattare con il metodo delle immagini facendo un'estensione (dispari o pari, a seconda delle condizioni di bordo di Dirichlet o Neumann) dei dati iniziali.

      Per trattare problemi su un intervallo e` molto piu` comodo usare il metodo (piu` potente) di decomposizione di Fourier. 

      Abbiamo descritto come usare questo metodo per problemi con condizioni di bordo omogenee e condizioni iniziali arbitrarie.

      Esercizio lasciato da provare: risolvere l'equazione delle onde su intervallo [0,3] con condizioni di bordo di Neumann, e con dati iniziali specificati da u(x,0) = sin^2(Pi x/3) , e u_t(x,0) = Cos[ 2 Pi x/3] .

    • registrazione URL


    • Fenomeno della risonanza: ampiezza delle oscillazioni in funzione del tempo per una soluzione soggetta a un termine forzante oscillante con frequenza molto vicina a una delle frequenze caratteristiche del sistema. La soluzione mostra oscillazioni amplicata con ampiezza crescente nel tempo.

  • Collapse Expand

    Lezione 19 - Problemi di bordo non omogenei

    • Abbamo discusso con alcuni esempi come trattare, con il metodo di Fourier, problemi di bordo non omogenei per l'equazione delle onde nella forma piu` generale con anche un termne forzante non omogeneo.

      Abbamo usato un esempio di soluzione di problema con termine forzante per discutere il fenomeno della risonanza per l'equazione delle onde.

      Alla fine della lezione abbiamo iniziato a discutere l'equazione del calore, dando la sua derivazione dalla legge di conduzione del calore di Fourier. 


    • registrazione URL
  • Collapse Expand

    Lezione 20 - equazione del calore

    • Abbiamo discusso alcune proprieta` dell'equazione del calore, e come risolvere problemi di bordo con il metodo di Fourier, discutendo alcuni esempi.

      - soluzione fondamentale equazione del calore (heat kernel).

      - soluzione problema in spazio infinito con condizione iniziale arbitraria

      -soluzione problema in spazio inifnito con temrine inomogeneo tramite funzione di Green (e sua relazione con la soluzione fondamentale)

      - proprieta` matematiche: differenziabilita`  infinita delle soluzioni anche per dati iniziali irregolari, e velocita` di propagazione infinita dei segnali.

      -problemi di bordo (Dirichlet e Neumann) e loro significato fisico

      -metodo di soluzione dei problemi di bordo su un intervallo attraverso il metodo di Fourier.

      -Abbiamo discusso il metodo di Fourier per 3 problemi. 

      1. Problema su un intervallo con condizioni di bordo di Dirichlet (bordi a temperatura 0 ) e condizione iniziale uniforme a temperatura costante T1.

      2. Problema con condizioni di bordo omogenee di Neumann. Abbiamo visto come il limite della temperatura dopo un tempo infinito e` legato al dato iniziale dalla conservazione dell'energia termica

      3. Problema con condizioni di bordo dipendenti dal tempo.

      Questi problemi sono i problemi 3),4),5)  illustrati sul file Mathematica allegato.



    • Soluzione fondamentale: 


    • esercizi illustrati in Mathematica File
    • file Mathematica
  • Collapse Expand

    Lezione 21 - equazione di Burgers con viscosita` e inizio PDE in D>1.




    • Abbiamo discusso come risolvere esplicitamente l'equazione di Burgers con un termine di viscosita`, tramite una mappa su soluzioni dell'equazione del calore che abbiamo risolto esplicitamente con il metodo dell' "heat kernel".  La soluzione ha una forma integrale, e abbiamo notato che il limite di piccola viscosita` di questa soluzione si puo` trattare con il metodo del punto a sella. Studiando questo limite abbiamo discusso come l'equazione con piccola viscosita` approssima la soluzione con fronti di shock discontinui (si vedano figure sopra), con la posizione degli shock definita in modo da tagliare porzioni di area uguale della soluzione. Tale definizione corrisponde a quella che avevamo discusso in precedenza interpretando l'equazione di Burgers come legge di conservazione. 

      Abbiamo poi fatto alcuni commenti (fuori dal programma del corso) sul comportamento di un'equazione con termine sia nonlineare che dispersivo (derivata cubica): l'equazione di KdV. Il comportamento di questa equazione e il fenomeno delle eccitazioni solitoniche si puo` visualizzare nel video allegato nella sezione approfondimenti. 

      Infine, abbiamo iniziato a capire come risolvere PDE lineari su domini spaziali in piu` di una dimensione, con condizioni di bordo di Dirichlet o Neumann, piu` una direzione temporale. Abbiamo iniziato a trattare il caso dell'equazione del calore su un dominio rettangolare, ricavando la forma della soluzione come doppia serie di Fourier. 

    • video evoluzione equazione di KdV URL
    • Link a registrazione lezione URL
  • Collapse Expand

    Lezione 22 - Decomposizione in autofunzioni in D>1. Vibrazioni di un tamburo circolare.

    • Registrazione lezione scorso anno URL

    • Abbiamo continuato a descrivere come usare la generalizzazione del metodo di Fourier per risolvere l'equazione delle onde o del calore in dimensione spaziale D>1. Abbiamo descritto in dettaglio il caso di dominio rettangolare (che si generalizza al caso parallelepipedi) con le serie di Fourier in piu` variabili. Abbiamo considerato l'esempio del calcolo della soluzione per la diffusione di una goccia di inchiostro in una piscina rettangolare usando l'equazione di diffusione (=equazione del calore). 

      Abbiamo considerato il caso dell'equazione delle onde e calcolato le frequenze di vibrazione di una membrana rettangolare. 

      Abbiamo poi iniziato a spegare come caso del domnio dato dall'interno di un dominio circolare. In questo caso la decomposizione in autofunzioni dell'equazione di Helmoltz coinvolge le funzioni di Bessel (anche dette funzioni cilindriche).

      Abbiamo commentato il fatto che le frequenze di oscillazioni dei tamburi ideali di forma circolare o rettangolare non sono commensurabili l'una all'altra: quindi le oscillazioni non sono periodiche nel tempo, a meno che si riesca a eccitare un solo modo. Questo e` il motivo per cui un tamburo di solito produce un "rumore" invece che un suono di altezza (cioe` frequenza) definita: una condizione iniziale generica coinvolgera` sempre diversi modi di oscillazione che - quando sovrapposti - generano un segnale non periodico, e quindi non riconoscibile come suono di altezza definita.


  • Collapse Expand

    Lezione 23 - inizio equazione di Laplace

    • Link a registrazione URL

    • Abbiamo finito di discutere il metodo delle autofunzioni generalizzato per le equazioni di Laplace o del calore, discutendo come decomporre i dati iniziali su un insieme di autofunzioni generico, che venga dalla soluzione dell'equazione di Helmholtz in un dominio generico con condizioni di bordo di Dirichlet o di Neumann omogenee. 

      Abbiamo trattato esplicitamente il caso di una membrana circolare, discutendo come decomporre dati generici nelle autofunzioni corrispondenti, che avevamo ricavato la lezione precedente e sono collegate alle funzioni di Bessel.

      Abbiamo poi iniziato a discutere l'equazione di Laplace o Poisson, discutendone alcune applicazioni e alcune proprieta`  matematiche delle soluzioni.

  • Collapse Expand

    Lezione 24 - Laplace e Poisson con separazione delle variabili e funzioni di Green

    • Abbiamo discusso come risolvere l'equazione di Laplace con condizioni di bordo di Dirichlet generiche per tre tipi di domini: dominio rettangolare, dominio definito dall'interno di un disco, dominio definito da una corona circolare.

      Abbiamo poi discusso il metodo delle funzioni di Green per le equazioni di Laplace e Poisson. Abbiamo derivato le funzioni di Green per il problema in spazio infinito in dimensioni D=2 e D=3, e abbiamo poi descritto la formula di rappresentazione delle soluzioni in un dominio finito ottenuta usando le identita` di Green.

      Infine, abbiamo descritto la nozione di funzione di Green per un dominio spaziale finito generico. Abbiamo infine descritto esplicitamente un caso particolare in cui questa funzione di Green si puo` trovare con il metodo delle immagini: la funzione di Green per il dominio definito da un semipiano in D=2.